Principe de compression des données en mémoire de Prometheus
À propos
Cet article n’a pas vocation à faire du lecteur un expert dans l’écriture de base de données de séries temporelles. En revanche, ce document aidera à comprendre comment sont stockées les données et vous fournira une partie des techniques utilisées pour réduire les besoins en ressources dans le cas de Prometheus. Ils aideront également à appréhender les limitations inhérentes à ce type de base de données (notamment pourquoi il est compliqué de modifier une donnée après insertion).
Cet article abordera les concepts suivants qui sont nécessaire à la compréhension des techniques de compression utilisées :
- la représentation au format binaire ou hexadécimal
- le stockage de valeurs entières
- le stockage de valeurs à virgule flottante
Pour mémoire, cet article a été écrit en préparation de mon livre sur Prometheus et Grafana sorti aux Éditions ENI. La fiche du livre est accessible à l’emplacement suivant : https://www.editions-eni.fr/livre/prometheus-et-grafana-surveillez-vos-applications-et-composants-systeme-9782409031748
La donnée dans Prometheus
Contexte
Prometheus utilise une base de données de type TSDB (Time Series DataBase). Cet acronyme se traduit en français par base de données de séries temporelles. Ce type de base de données n’est pas propre à Prometheus et il existe d’autres bases de données utilisant les mêmes concepts comme par exemple InfluxDB ou Timescale. Le premier est un logiciel libre de base de données dédié à l’utilisation de série temporelle et le second est une extension permettant de gérer des séries temporelles directement dans PostgreSQL.
Ces types de bases de données sont particulièrement adaptés au stockage de série de valeurs collectées à intervalle régulier. Toutefois, ce type de base n’est clairement pas adapté au stockage de données arbitraires. Il n’est ainsi pas possible de faire des schémas relationnels comme on pourrait le faire avec une base classique comme Postgres.
Dans le monde des séries temporelles, Gorilla est un outil souvent mentionné. Pour ceux qui ne connaissent pas, il s’agit d’un projet interne de Facebook/Meta et qui a pour but de permettre la collecte de métriques. Son fonctionnement interne a fait l’objet de publications et a servi de base pour des travaux sur les séries temporelles. N’hésitez pas à le consulter à l’adresse suivante (attention, le papier est en anglais) : https://www.vldb.org/pvldb/vol8/p1816-teller.pdf
Cycle de vie de la donnée
Prometheus est en mesure de collecter une grande quantité de métriques. Ces dernières passeront toutes par les étapes suivantes :
- Tout d’abord Prometheus consomme le point d’entrée d’un exporteur afin de récupérer un ensemble de métriques
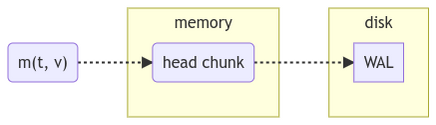
- Ces métriques passent par un tronçon de la base de données (chunk en anglais). Ce tronçon de travail est désigné généralement sous le terme HEAD (tête en anglais)
- Afin de se prémunir d’une perte de données, ces données sont également écrites dans le journal de transaction (WAL pour Write-Ahead-Log). À noter que l’accès à ces données se fait ensuite à l’aide d’un mécanisme de virtualisation d’accès mémoire (en anglais on parle de memory mapped I/O)
- Au bout d’un certain temps, ces blocs de données sont ensuite regroupés dans des blocs persistants sur disque. Ces blocs sont immuables et donc une fois créés, ils ne peuvent plus être modifiés (ou en tout cas très difficilement)
- Lorsque l’ensemble des données dans un bloc arrive à expiration, le bloc est supprimé. Par défaut, cette durée de rétention est de 15 jours
Remarque : Dans le langage de Prometheus, une grande quantité de métriques désigne généralement plusieurs millions de métriques. Il est même possible de consommer plusieurs dizaines millions de métriques par instance en réalisant quelques réglages. N’hésitez pas à vous reporter sur cet article pour plus d’infos sur ce sujet : https://blog.cloudflare.com/how-cloudflare-runs-prometheus-at-scale/
Ci-dessous un schéma reprenant cette description :
Données acquises par Prometheus
Un tronçon de données, ou chunk, est un espace mémoire tampon contenant les données en cours d’acquisition. La particularité de Prometheus est que le stockage de la donnée se fait directement dans un format compressé.
Ce format de compression s’appuie sur les caractéristiques des données acquises. Dans le cas de Prometheus, chaque point est stocké sous la forme suivante :
- Un horodatage (en anglais timestamp)
- La valeur collectée
Un horodatage (ou timestamp) représente un nombre de secondes écoulées depuis le 1er janvier 1970. Ce mécanisme de stockage est utilisé par exemple par les systèmes Unix pour connaître la date courante, on parle aussi d'heure Unix. Dans le cas de Prometheus, la valeur du temps est stockée avec une précision de l’ordre de la milliseconde sous la forme d’un entier sur 64 bits (structure int64).
Au niveau des valeurs, Prometheus ne manipule que des points sous forme de nombres à virgules flottantes (structure float64). Dans le cas où la donnée serait un entier, cette dernière sera convertie sous forme de flottant avant stockage.
Sans compression, chaque point consomme donc 8 octets pour l’horodatage et 8 octets pour la donnée soit 16 octets au total.
Référencement de la métrique
Afin d’accéder au contenu de ces valeurs, il est nécessaire de disposer d’un point d’entrée permettant de désigner la série. Il s’agit d’un nom arbitraire commençant par un caractère alpha et pouvant contenir une suite de caractères alphanumériques séparés par des tirets-bas (‘_’).
Ces noms respectent généralement un ensemble de bonnes pratiques – même si elles ne sont pas obligatoires, elles sont fortement encouragées – comme par exemple la notation Snake case et l’utilisation de suffixe pour désigner le contenu de la variable. Un compteur simple prendra par exemple le suffixe « _total » ou « _created ».
Lorsqu'il est nécessaire d’exposer une même métrique plusieurs fois, l’exporteur fera appel à la notion de labels. Ce type de solution est généralement utilisé pour regrouper les requêtes par catégorie d’erreur ou par contexte.
Les labels servent à identifier sa donnée. Ils peuvent commencer par un tirets-bas (‘_’). Dans ces cas-là, il s’agit généralement de labels réservés à un usage interne de Prometheus.
Ci-dessous un exemple de métriques référençant les appels HTTP sur les contextes « / » et « /api/v1 » ainsi qu’en fonction des codes http ‘200’ (la requête est ok) et 500 (erreur technique) :
http_requests_total{code="500",handler="/api/v1"} 1
http_requests_total{code="200",handler="/api/v1"} 20
http_requests_total{code="200",handler="/"} 45
Dans les faits, Prometheus stocke également le nom de la métrique sous la forme d’un label réservé : « __name__ ». Ces trois métriques seront donc en réalité stockées sous la forme suivante :
{__name__="http_requests_total",code="500",handler="/api/v1"} 1
{__name__="http_requests_total",code="200",handler="/api/v1"} 20
{__name__="http_requests_total",code="200",handler="/"} 45
Chaque série temporelle est associée à une entrée d’index comprenant ces labels. Prometheus maintient des index de recherche inverse afin de pouvoir retrouver des séries temporelles en fonction de leurs labels. Ici, les labels prennent environ 60 octets (longueur des chaînes de caractères) pour ces trois séries auxquels doivent s’ajouter les labels ajoutés automatiquement comme par exemple le label « job » (hérité du champ job_name de la configuration de surveillance) ainsi que le label « instance » pour désigner l’adresse du point de collecte.
À noter que la consommation d'espace mémoire des labels ne sera pas abordée dans cet article.
Projection d’utilisation de la mémoire
En ignorant cette entrée d’index, chaque point de la série temporelle prend 16 octets de place (sous la forme de disque ou mémoire principale). Pour une entrée collectée toutes les 15 secondes, la quantité de place utilisée devrait évoluer de la manière suivante :
- 4 x 16 octets = 64 octets par minute
- 64 x 60 = 3 840 octets par heure
- 3 840 x 24 = 92 160 octets par jour
- 92 160 x 15 = 1 382 500 octets pour 15 jours de rétention (rétention par défaut)
Ici, la donnée devrait consommer 1,3 Mo de place par série temporelle (ou métrique) sur 15 jours.
Le point d’entrée des métriques de Prometheus génère à lui seul environ 500 séries temporelles:
- Consommation mémoire
- Nombre d'appels d'API
- Taille des blocs
- Etc.
On devrait donc logiquement consommer 500 x 1,3 Mo = 650 Mo de données pour 15 jours de rétention alors que nous n’avons même pas commencé à démarrer la collecte de points d’entrées externes.
Caractéristiques de la données
Dans les faits, cette valeur n’est jamais atteinte car Prometheus utilise des mécanismes de compression sur ses séries temporelles. Pour cela, il s’appuie sur les caractéristiques suivantes :
- Les collectes se font avec une fréquence constante
- Les valeurs collectées varient peu entre deux échantillonnages
Un bon moyen de s’en convaincre est de prendre un premier exemple avec la métrique up. Cette dernière est utilisée pour vérifier qu’une collecte s’est bien passée. Cette valeur est collectée toutes les 15 secondes et porte toujours la valeur 1.
Le nombre total de requêtes est un autre exemple de métriques disponible par défaut. Dans le cas de Prometheus, il existe une métrique correspondant aux appels faits sur le point d’entrée des métriques (http://localhost:9090/metrics). Cette métrique porte le nom de « promhttp_metric_handler_requests_total » (pour la suite, elle sera référencée sous le nom de « Nb appels »). La caractéristique de cette valeur est de s’incrémenter de 1 à chaque collecte.
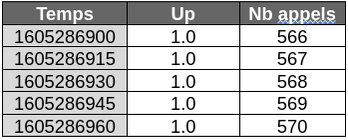
Ci-dessous un exemple de mesures pouvant correspondre à ces descriptions :
Delta et double delta
En observant les données de l'exemple précédent, on constate que les valeurs sont toutes identiques pour « Up » (1.0) ou évoluent par pas de 1 pour « Nb appels ». L’horodatage, quant à lui, évolue de manière uniforme par pas de 15 secondes.
Cette évolution se note sous la forme d’une différence (ou delta entre deux valeurs). Par la suite, ce delta pourra être noté à l’aide de la lettre grec du même nom (symbole « Δ »). Cette opération sera seulement appliquée que sur l’horodatage. La compression des valeurs collectées sera abordée dans un second temps.
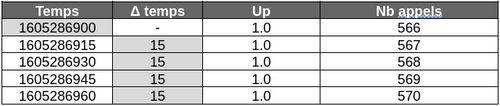
Ci-dessous le même tableau de valeur avec le delta entre chaque horodatage :
Dorénavant, en dehors de la première collecte, le delta temps entre chaque collecte est identique. En continuant dans cette logique, il est possible de calculer la différence de la différence ou delta de delta (noté ΔΔ) des temps d’horodatages.
Ci-dessous le tableau mis à jour avec ces nouvelles valeurs :
Cette fois-ci, à partir de la 3ème collecte, les delta de delta restent toujours à zéro. Cette caractéristique est particulièrement intéressante puisque lorsque ces conditions sont réunies, il devient possible d’appliquer certaines techniques de compression directement sur la donnée en mémoire.
Encodage des entiers en informatique
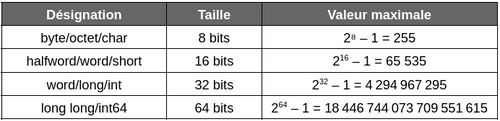
En informatique, un entier est stocké sous la forme d’une suite de 0 et de 1 dans des structures de plus ou moins grande taille. Un octet (ou byte en anglais) est ainsi composé d’une suite de 8 bits. On s’en sert généralement pour stocker des caractères alphanumériques mais on peut également s’en servir pour stocker des entiers d’une valeur pouvant varier de 0 à 255 (soit 256 possibilités). Pour stocker des plages de valeurs plus grandes, il suffit de concaténer ces octets et passer à des compteurs sur 2 octets (16 bits), 4 octets (32 bits) ou 8 octets (64 bits).
En informatique, ces structures sont généralement désignées sous le terme de mot (word). Ce mot peut prendre des tailles différentes et plus le mot sera grand, plus ce dernier permettra de stocker une grande valeur. N’hésitez pas à consulter l’article de Wikipedia sur le sujet pour en apprendre plus : Mot (article Wikipedia)
La taille maximale qui peut être représentée dans un entier dépend de la valeur de n qui représente la taille du mot exprimée en bits. Elle s’exprime sous la forme suivante :
Un mot sur 16 bits permettra ainsi de stocker des valeurs maximales de 65535
Ci-dessous quelques exemples de mots informatiques classiques que l’on peut rencontrer en C, Java ou Go :
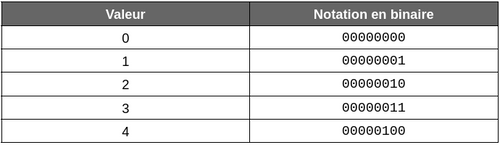
L’incrémentation commence par les bits de droites et les autres bits restent à 0. Ci-dessous quelques exemples d’écriture d’entier décimaux en binaire sur 8 bits :
L’avantage d'utiliser une taille fixe est qu’il est très facile de manipuler les chiffres et de les additionner entre eux. En revanche, on se rend compte que dans les exemples donnés, les 0 en début de nombre prennent quasiment toute la place alors qu’ils n’apportent aucune information.
Encodage des nombres réels en informatique
En informatique, la représentation d’un réel s’appuie sur la notation scientifique. Cette notation a pour principe de normaliser l’écriture des nombres sous la forme suivante :
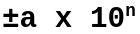
Ci-dessous la définition des éléments de cette fonction :
- ± : signe du nombre
- a : mantisse compris dans l’intervalle [1,10[ (10 est exclu)
- n : exposant
Et ici quelques exemples de conversion :
Pour l’essentiel, le stockage des valeurs à virgules flottantes utilise le même principe à la différence que le stockage ne se fait pas avec des nombres en base 10 (ou décimaux) mais en base 2 (binaire).
Autre point, le stockage des nombres réels se fait à l’aide de mots. Tout comme pour la notation scientifique, le mot est découpé en trois parties :
- le signe du réel
- une mantisse (fraction en anglais)
- un exposant (exponent en anglais)
N’hésitez pas à vous reporter à l’article Wikipedia suivant pour approfondir le sujet : https://fr.wikipedia.org/wiki/Virgule_flottante
En informatique, ces valeurs à virgules flottantes sont stockées dans des mots de 32 bits (4 octets) pour la simple précision ou 64 bits (8 octets) pour la double précision. La structure de ces nombres est régie par la norme IEEE 754. Cette dernière définit les découpages suivants :
Par convention, les chiffres écrits au format binaire sont préfixés par la chaîne ‘0b’.
Ci-dessous un exemple de représentation au format binaire de la valeur 1,0 sur 32 bits :
0b00111111100000000000000000000000
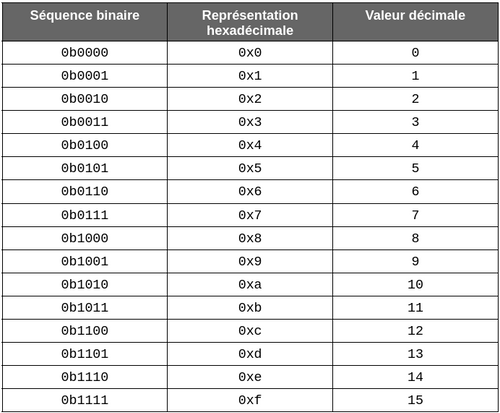
Afin de gagner en clarté, la notation hexadécimale sera préférée pour la suite des exemples. Cette représentation consiste à regrouper les bits d’un mot informatique par groupe de 4 et à utiliser une représentation sur une base 16 en utilisant les chiffres 0 à 9 pour les 10 premiers chiffres ainsi que les lettres A à F pour les 6 suivants.
À noter que les séquences hexadécimales commencent toutes par les caractères ‘0x’.
Ci-dessous un tableau de correspondance entre la représentation binaire d’une séquence de 4 bits et la notation hexadécimale :
Pour augmenter la taille du mot, il suffit d’ajouter des caractères hexadécimaux. Ainsi, un octet (8 bits) sera représenté par 2 chiffres hexadécimaux, 4 chiffres pour un entier sur 16 bits, 8 chiffres hexadécimaux pour un entier sur 32 bits et enfin 16 chiffres pour un entier sur 64 bits.
Par la suite, les exemples se feront avec des valeurs sur 32 bits dans des soucis de clarté et de concision. Ces principes s’appliquent de la même manière avec des chiffres sur 64 bits, précision utilisée en interne par Prometheus.
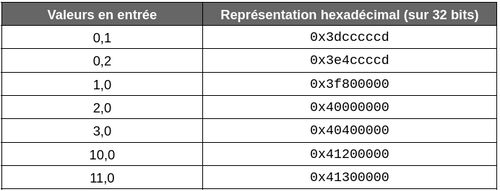
Ci-dessous quelques exemples de représentations hexadécimales de valeurs à virgules flottantes sur 32 bits :
Il est intéressant de constater que les valeurs proches le sont également dans leurs représentations hexadécimales. Cette caractéristique va permettre d’appliquer des techniques de compression. Dans le cas de Prometheus, ce dernier fait appel à l’opérateur XOR pour y parvenir.
Technique de compression de la donnée en mémoire
Tronçons actif
Prometheus utilise des tronçons compressés (compressed chunk en anglais) pour stocker sa donnée en mémoire. Cette dernière est toujours écrite dans le tronçon actif au niveau du premier emplacement. Par défaut, dans Prometheus, une fois une valeur écrite, il n’est plus possible de la modifier ou de changer une valeur antérieure (cette partie sera détaillée plus loin dans l'article).
Au bout d’un certain temps, le tronçon actif se remplit et est remplacé par un nouveau tronçon. Ce tronçon est considéré comme complet s’il remplit une de ces conditions :
- il contient 120 mesures (couple horodatage, valeur)
- la plage de temps qu’il couvre est supérieure à 2 heures
Lorsqu’un de ces événements se produit, un nouveau tronçon est créé et vient remplacer le précédent.
Ces précédents blocs peuvent se trouver en mémoire ou sur disque. L’accès se fait à l’aide du mécanisme de virtualisation d’accès mémoire.
Stockage des nombres entiers dans Prometheus
Pour compresser sa donnée en mémoire, Prometheus fait appel à la notion de codage de valeur à largeur variable (en anglais variable bit-width encoding). On parlera également d'un flux de bits.
Dans le cas de l’horodatage, pour faire cette écriture, la convention suivante est utilisée :
- Si ΔΔ est égal à 0, on positionne un bit à 0
- Si ΔΔ est inférieur à 213 (8,192 ms), on positionne les bits ‘10’ suivi d’une valeur sur 14 bits
- Si ΔΔ est inférieur à 216 (65,536 ms), on positionne les bits ‘110’ suivi d’une valeur sur 17 bits
- Si ΔΔ est inférieur à 219 (524,288 ms soit environ 8 minutes), on positionne les bits ‘1110’ suivi d’une valeur sur 20 bits
- Enfin, si ΔΔ est supérieur, on positionne les bits ‘1111’ suivi de la valeur sur 64 bits
Cet algorithme se retrouve dans le code source de Prometheus dans le fichier tsdb/chunkenc/xor.go. Ci-dessous un extrait du code en question :
// Gorilla has a max resolution of seconds, Prometheus milliseconds.
// Thus we use higher value range steps with larger bit size.
switch {
case dod == 0: // dod = delta of delta
a.b.writeBit(zero)
case bitRange(dod, 14):
a.b.writeBits(0x02, 2) // '10'
a.b.writeBits(uint64(dod), 14)
case bitRange(dod, 17):
a.b.writeBits(0x06, 3) // '110'
a.b.writeBits(uint64(dod), 17)
case bitRange(dod, 20):
a.b.writeBits(0x0e, 4) // '1110'
a.b.writeBits(uint64(dod), 20)
default:
a.b.writeBits(0x0f, 4) // '1111'
a.b.writeBits(uint64(dod), 64)
}
Cette technique fonctionne seulement avec le stockage d’entier, la compression des valeurs à virgules flottantes (float64) sera abordée un peu plus loin.
Comme Prometheus gère l'intervalle de collecte, la valeur ΔΔ prend souvent la valeur 0. La série des horodatages a donc de grande chance d’être une suite de bit à 0 prenant très peu de place. En cas de non variation, la consommation d'espace mémoire sera réduite d'un facteur 64.
Dans le cas un peu moins favorable où la collecte n’aurait pas été réalisée au bon moment à quelques secondes près (moins de 8 secondes), la place prise sera de 16 bits (soit 2 octets). La réduction sera ici 4 fois inférieure (ce qui reste intéressant).
Dans le cas d’une collecte se faisant une minute plus tard, la consommation de place sera de 3 octets (toujours à comparer au 8 octets initialement utilisé par un stockage brut).
Le dernier cas sera en revanche plus coûteux puisque la consommation de place sera de 68 bits contre 64 bits pour une valeur brute.
Dans les faits, les deux premiers représentent l’essentiel des cas et les cas suivants se produisent à une fréquence très faible.
Stockage des valeurs à virgules flottantes dans Prometheus
Opérateur logique XOR
La fonction XOR (ou fonction OU exclusif) désigne un opérateur logique de l’algèbre de Boole. Cette fonction prend deux valeurs en entrée à la valeur VRAI ou FAUX et renvoie la valeur VRAI seulement si les deux entrées ont des valeurs différentes et FAUX dans le cas contraire.
Cette fonction est traditionnellement utilisée en électronique, informatique mais également en cryptographie du fait de ses propriétés. Par la suite, l’opération sera notée à l’aide du symbole ‘⊕’.
Dans le cas de Prometheus, cette fonction va être utilisée afin de ne garder que les parties qui varient entre deux échantillonnages. L’aspect intéressant est qu’il devient possible d’obtenir les valeurs existantes en partant de la valeur initiale et en y appliquant le résultat de l’opération ⊕ (xor). Ainsi pour les échantillonnages successifs m[1], m[2] ainsi que la valeur r[1] correspondant au résultat de l’opération ⊕, il est possible d’écrire les égalités suivantes :
Pour poursuivre dans cette logique, si on prend une suite d’échantillonnages ainsi que le résultat de l’opération ⊕, il est possible d’écrire les égalités suivantes :
Il est donc possible de récupérer les échantillonnages initiaux en ne stockant que les valeurs xor.
Reste à comprendre en quoi ceci est intéressant en observant le résultat de l’opération appliquée à des exemples de couples d’échantillonnages successifs :
À première vue, la représentation hexadécimale du résultat est constituée en grande partie d’une suite de 0 en début et/ou fin. Dans le cas où l’échantillonnage ne varie pas, le résultat sera entièrement constitué de 0. Ces caractéristiques vont encore une fois permettre de réduire la consommation de mémoire.
Stockage de la valeur initiale et absence de variation
La valeur initiale ne pouvant être compressée, elle sera toujours stockée directement dans le flux de bits.
Le premier cas particulier à traiter sera évidemment le cas d’une valeur xor égale à 0. Dans ce cas, un bit à 0 est ajouté dans le flux de bit et l’opération est terminée.
Introduction d’une fenêtre de la donnée
Reste maintenant à adresser les autres cas. Pour cela, la compression va s’appuyer sur la notion de fenêtre pour réduire la quantité de mémoire utilisée. En effet, le résultat de l’opération xor suit généralement le schéma suivant :
- Un ensemble de zéros initiaux
- Une suite de valeurs significatives
- Un ensemble de zéros
Une fenêtre va permettre de supprimer les parties inutiles en début et fin de mot. Ne restera plus qu’à stocker directement dans le flux de bits la partie significative.
Pour définir une nouvelle fenêtre, la suite de bits ‘11’ (on parlera par la suite d'entête) sera utilisée suivie des éléments suivants :
- Le nombre de zéros initiaux (sur 5 bits pour une valeur decimal maximale de 2⁵ – 1 = 31)
- Le nombre de valeurs significatives (sur 6 bits pour une valeur decimal maximale de 2⁶ – 1 = 63)
- L’ensemble des bits correspondants à la partie significative
La structure décrite ici est adaptée à la représentation sur 64 bits et non sur 32 bits. Il serait tout à fait possible de réduire de 1 bits ces compteurs pour être adaptés à une structure sur 32 bits et ainsi gagner 2 bits supplémentaires. Tout ceci reste un exercice qui permet de comprendre la technique de compression.
Ci-dessous une représentation de cette fenêtre pour l’opération xor sur les valeurs 1535,0 et 1513,0 (0x0002c000 en hexadécimal) :
Ici, la fenêtre minimale permettant de représenter ce chiffre possédera les caractéristiques suivantes :
- 14 zéros initiaux représentés à l’aide de 5 bits soit : ‘01110’
- 4 bits significatifs représentés à l’aide de 6 bits soit : ‘000100’
À ces éléments, il sera également nécessaire d’ajouter les suites de bits suivantes :
- La définition d’une nouvelle fenêtre avec les bits ‘11’ en début de flux
- La partie significative sous la forme ‘1011’ en fin de flux
En combinant toutes ces indications, le flux binaire suivant pourra être utilisé pour la représentation du nombre hexadécimal 0x0002c000 :
Ci-dessous le récapitulatif de ces éléments :
- Entête de définition de la fenêtre (11)
- 5 bits représentant la valeur décimale 9 en binaire (00101)
- 6 bits représentant la valeur décimale 2 en binaire (000010)
- 4 bits représentant les bits significatifs (1011)
Ici, la valeur stockée ne nécessite que 15 bits contre 32 bits pour la version non compressée.
Réutilisation de la fenêtre et exemple de flux de bits
Dans les faits, la fenêtre qui vient d’être définie a rarement besoin d’être redéfinie. Dans ce cas, il suffit d’injecter l'entête avec les bits ‘10’ dans le flux de bits suivi des bits significatifs.
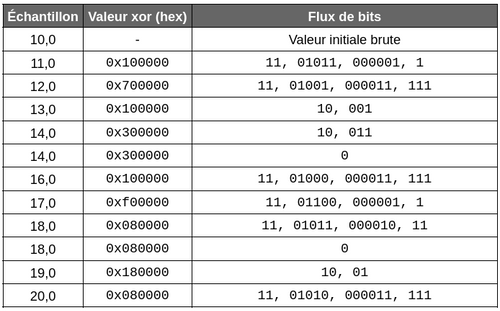
Ci-dessous un exemple de valeurs – pour chacune de ces valeurs – la valeur xor correspondante ainsi que le flux de bits généré :
Ces valeurs ont été générées à l’aide d’un petit programme Python reproduisant le fonctionnement de l’algorithme de Prometheus. Afin de reproduire ces résultats, je vous invite à lancer le programme generate_bit_stream.py (disponible à cet emplacement : https://github.com/EditionsENI/prometheus-grafana/blob/main/annexes).
Ici, ces douze valeurs ont généré un flux de 139 bits soit environ 17,4 octets au total. Ces mêmes valeurs stockées dans des nombres à virgules simple précision prennent 4 octets x 12 = 48 octets soit 384 bits. Dans le cas présent, le ratio de compression est donc de 384 / 139 ≈ 2.
Quelques éléments de statistiques
Dans les faits, les événements décrits précédemment se produisent aux fréquences suivantes :
- Pas de variation (soit écriture d’un bit à 0) dans environ 50 % des cas
- Réutilisation d’une fenêtre de transmission dans environ 30 % des cas
- Définition d’une fenêtre puis transmission dans les 20 % restant
Ces chiffres sont extraits d’un papier sur le fonctionnement de Gorilla (cf https://www.vldb.org/pvldb/vol8/p1816-teller.pdf). Tout ceci doit donc être pris avec recul et devra être confirmé à chaque utilisation réelle.
Au final, chaque mesure consomme en moyenne entre 1 et 2 octets (contre 16 octets pour la donnée brute). Ces mécanismes permettent de réduire la consommation mémoire d’un facteur de l’ordre de 10.
Pour conclure
Comme nous avons pu le voir, Prometheus combine plusieurs techniques pour la compression de ses données :
- Le delta de delta pour le stockage de l’horodatage
- L’opération XOR entre échantillons afin de déterminer les changements
- Le stockage à bits variables (implémenté via le mécanisme de fenêtre)
Dans un usage classique, comme indiqué un peu plus haut, la combinaison de ces techniques permet de réduire d’un facteur 10 la consommation de mémoire.
Toutefois ces opérations engendrent une complexité importante pour toute modification des données dans le passé. En effet, comme les données actuelles dépendent des précédentes, toute insertion rétroactive impose au moteur de récupérer les valeurs existantes, d’insérer la nouvelle donnée et de recalculer la suite. Par défaut, Prometheus bloque ce type d’opération et son activation nécessite le démarrage avec une option spécifique.
Un autre point clé réside dans la réorganisation régulière des données : toutes les deux heures, Prometheus réarrange ses informations collectées pour les stocker sous forme de fichiers immuables (compactions). Cette technique limite les accès disque en regroupant les données en blocs plus larges, mais rend aussi les modifications ou suppressions de données très complexes : Il faut récupérer le bloc, extraire les données, les modifier avant de recréer le bloc.
Dans les faits, cette limite est rarement problématique. En effet, les données de surveillance n'ont généralement pas vocation à être modifiées une fois collectées. De mon point de vue, l’immuabilité des données est même un atout, rendant Prometheus fiable pour les audits et les environnements sensibles où la préservation des traces historiques est essentielle.
Un autre aspect intéressant de cette approche est l’impact positif de la compression sur l’ensemble des ressources système. Bien que cette technique impose un certain coût CPU, elle permet une réduction notable de l’empreinte mémoire totale et des accès disque. Ce gain de ressources se traduit par une capacité accrue pour d’autres opérations (mise en cache, augmentation du nombre de métriques en mémoire, etc.), ce qui améliore les performances globales de Prometheus.
Enfin, Prometheus emploie d’autres techniques pour réduire sa consommation de ressources, telles que la déduplication des chaînes de caractères et l’indexation avancée. Chacune de ces optimisations mériterait un article dédié pour explorer en détail les techniques mises en œuvre. Tout ceci contribue au fait que Prometheus est devenu un outil incontournable et adapté aux environnements de surveillance modernes.


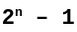
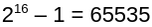
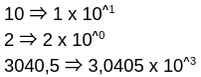


![m[1] ⊕ m[2] = r[1]
m[1] ⊕ r[1] = m[2]
m[2] ⊕ r[1] = m[1]](/principe-de-compression-des-donnees-en-memoire-de-prometheus/image18_resize.jpg)
![m[2] = m[1] ⊕ r[1]
m[3] = m[2] ⊕ r[2]
m[4] = m[3] ⊕ r[3]
…
m[n] = m[n-1] ⊕ xor[n-1]](/principe-de-compression-des-donnees-en-memoire-de-prometheus/image19_resize.jpg)

![0b[00000000000000][1011][00000000000000]](/principe-de-compression-des-donnees-en-memoire-de-prometheus/image21_resize.jpg)
![0b[11][01110][000100][1011] = 0b11011100001001011](/principe-de-compression-des-donnees-en-memoire-de-prometheus/image22_resize.jpg)