Online Machine Learning - Application à la publicité sur le web

L'apprentissage en ligne automatisé (ou online machine learning) est une section du machine learning utilisée pour générer un modèle en apprenant au fur et à mesure. On oppose ce style d'apprentissage à l'utilisation de batchs sur de grandes quantités de données. Il devient alors important d'enrichir le modèle dynamiquement dès qu'une nouvelle donnée arrive.

C'est dans ce cadre que l'University College London a lancé il y a deux ans un challenge pour prédire la meilleure publicité à présenter à un visiteur web, meilleure au sens de celle ayant la plus grande probabilité qu'il clique dessus. Voici une description des conditions et règles de ce challenge auquel j'ai pu participer, ainsi que quelques pistes pour résoudre le problème.

Quelques éléments métier

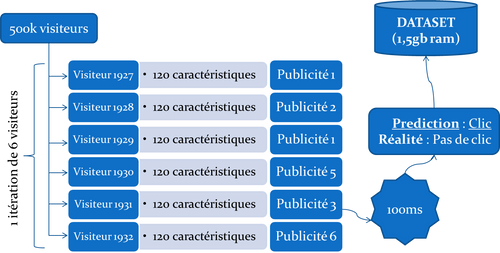
Imaginons six visiteurs arrivant sur une page web. Pour chaque visiteur, nous disposons de 120 caractéristiques numériques le décrivant ainsi que de la publicité parmi les 6 qui lui ont été proposées. Compte tenu de ces informations, il faut choisir parmi les 6 visiteurs celui qui a le plus de chance de cliquer sur sa publicité. Autrement dit, on choisit le visiteur dont on aurait prédit le mieux la publicité qui lui a été proposée.

Il est bien entendu impossible de savoir à l'avance la typologie des visiteurs que nous allons accueillir. Nous disposons tout de même pour l'initialisation de l'algorithme des 100 premiers visiteurs, de la publicité qui a été proposée à chacun et du clic le cas échéant. Nous attendons 20 millions de visiteurs et nous savons que le taux de clic ou CTR (Click-Through Rate) est très faible (0,24%). Il y aura donc très peu d'exemples positifs (des clics) pour réaliser l'apprentissage.

Nous sommes donc dans un contexte où les données initiales sont quasi-inexistantes. Il est donc impossible de construire a priori un modèle robuste. Le modèle sera par conséquent construit automatiquement au fur et à mesure. Tout travail de data science (création et sélection de features, nettoyage du set d'apprentissage etc...),  est rendu difficile par l'absence de signification des caractéristiques (celles-ci n'ont pas de label dans le fichier csv fourni et donc pas de sens métier) et par le manque de données initiales.

Quelques éléments techniques

Le challenge fournit aux participants un csv contenant les caractéristiques des 100 premiers visiteurs, l'information de la publicité proposée et le clic, le cas échéant.

Il est également fourni un début de template en Java et il est donc attendu un jar à soumettre sur la plateforme du challenge. La plateforme soumet les algorithmes des participants aux 500 000 premiers visiteurs et renvoie un score donné par le nombre de clics correctement prédits. Cette soumission est composée d'itérations simulant chacune 6 visiteurs arrivant en même temps, ce qui nous donne à peu près 80 000 itérations au total. On ne choisit qu'un seul visiteur par itération, et on ne dispose de l'information du clic que pour le visiteur choisi. L’exécution de chaque itération ne doit pas dépasser 100ms. Les algorithmes sont classés et sélectionnés à l'issue de cette première phase de deux mois durant laquelle les participants soumettent régulièrement et améliorent progressivement leurs algorithmes. Puis les trois meilleurs algorithmes sont soumis une seule fois aux 19,5 millions de visiteurs restants (phase de validation) et donc définitivement classés. Le code doit être single-threadé et ne doit pas consommer plus de 1,5 gb de RAM.

Il faut donc un algorithme qui se concentre sur les données récentes (temps d'exécution limité) tout en ayant pré-digéré/modélisé le passé.

La raison du découpage des données en deux jeux (de 500.000 et 19,5 millions de visiteurs) et de leur disproportion est d'éviter le sur-apprentissage durant la première phase.

De plus, il n'y a ici à proprement dit pas de set d'apprentissage et de set de test. Chaque donnée arrivant est considérée comme du set de test. Puis lorsque le résultat de la prédiction est dévoilé, la donnée passe du côté du set d'apprentissage car elle est alors utilisée pour composer le modèle qui servira aux données suivantes.

Quelques éléments de réponse :

Je ne me focaliserai pas dans cet article sur la mise en relation du vecteur de 120 colonnes (le visiteur) avec un choix qui peut prendre 6 valeurs (les publicités) et décider le meilleur couple visiteur-publicité. Voici un autre aspect, plus théorique, du problème tel que j'ai essayé de le résoudre :

1. Le dilemme exploration-exploitation

Chaque donnée (120 caractéristiques d'un visiteur, la publicité proposée et l'information clic/pas clic) acquise vient s'ajouter au set d'apprentissage disponible. Le modèle d'apprentissage a en principe été enrichi. Ainsi, lorsqu'un nouveau visiteur a été choisi, deux stratégies sont possibles :

• Se baser sur les connaissances acquises et miser sur le couple visiteur-publicité qui a le plus de chances de succès. C'est-à-dire tenter de récolter dès à présent le fruit du travail réalisé dans le passé - ie exploiter.
• Chercher à compléter la base de connaissance en explorant des possibilités non encore vues, c'est-à-dire des publicités peu probables au regard du profil du visiteur. On prend le risque de se tromper tout en sachant que la connaissance nouvellement acquise (il a cliqué alors qu'on ne s'y attendait pas ou bien il n'a pas cliqué et on le savait déjà donc maintenant c'est sur) nous permettra de choisir plus efficacement dans le futur.

Voici un algorithme très efficace au regard de sa simplicité et résolvant ce problème : Epsilon-greedy

Etant donné :

• ε, facteur de découverte entre 0 et 1
• i_n la publicité la plus probable (ou plus généralement un bras) d'indice i au temps n

Je choisis d'explorer une publicité aléatoire avec probabilité ε et d'exploiter la publicité la plus probable avec probabilité 1-ε. De nombreuses variantes existent et consistent à faire varier epsilon, ou la durée de la phase d'exploration. Prenons par exemple :

Algorithme : Epsilon_n-greedy Il paraît logique d'explorer de moins en moins avec le temps. Il faut faire varier ε comme 1/n (n étant le numéro de l'itération) en posant ε_n facteur de découverte au temps n, a étant un facteur à ajuster :

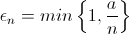
Je choisis d'explorer une publicité aléatoire avec probabilité ε_n, et d'exploiter la publicité optimale avec probabilité 1-ε_n.

Nous venons de voir une stratégie pour équilibrer exploration/apprentissage de nouvelles données et exploitation des connaissances acquises. Voici à présent une autre stratégie ne faisant plus intervenir d'aléatoire et permettant de réaliser un meilleur trade-off de l'exploration/exploitation avec la supposition suivante :

Imaginons le même problème sans avoir les caractéristiques du visiteur, c'est-à-dire en prenant comme supposition qu'il existe une publicité parmi les 6 meilleure que les autres, et que le clic se fait indépendamment des caractéristiques du visiteur.

2. Le bandit à plusieurs bras

Dans un environnement inconnu, il faut se constituer un premier set de données avant d'espérer prendre des décisions correctes. Malheureusement, ici ce set de données arrive au fur et à mesure et est dépendant de la prédiction faite : Nous prédisons une publicité parmi 6 (associée à son visiteur) puis nous apprenons si le visiteur a cliqué, mais nous ne savons pas ce qu'il en aurait été des cinq autres couples visiteurs-publicités. D'une certaine façon, nous choisissons notre dataset. Si nous prédisons toujours la publicité 1, notre dataset ne sera constitué que d'informations sur la publicité 1.

On appelle ce type de problème le bandit-manchot à plusieurs bras. Il faut choisir un bras à tirer (ce qui correspond dans notre cas à un couple visiteur-publicité entre 6) et observer le résultat, ne sachant pas ce que les autres bras auraient donné. L'observation est par essence incomplète. Peut-être personne sur les 6 visiteurs n'a cliqué sur sa publicité et dans tous les cas, notre prédiction aurait été correcte (cela arrive souvent).

Q° : Comment choisir parmi les différents bras de manière à minimiser asymptotiquement les clics mal prédits ?

Algorithme classique : UCB pour Upper Confidence Bound Chaque publicité est scorée (nombre de clics) avec une marge d'erreur statistique. L'estimation de l'erreur possible est donnée par l'intervalle de confiance. Plus celui-ci est grand, et plus l'incertitude sur le score est grande.

UCB dans sa version UCB-1 dicte qu'il faut choisir le bras-publicité dont la somme du score et de la marge d'erreur est la plus grande. C'est une version optimiste car elle considère que :

• Si un bras ne donne pas de clic, on aura au moins gagné de l'information et réussi à faire diminuer sa marge d'incertitude car il aura été testé. Par conséquent, il sera moins testé dans les prochaines itérations.
• Si un bras est vainqueur, de la même façon, la marge d'incertitude diminue mais le score lui augmente. Ce bras sera donc amené à être encore testé dans le futur.

Le trade-off exploration/exploitation est ici résolu par l'adaptativité de notre choix à la somme du score et de la marge d'erreur des différents bras. Dans tous les cas, choisir un bras diminue l'incertitude et affine la décision. La somme du score et de la marge d'erreur est donc un bon compromis pour équilibrer ce trade-off.

Décrivons l'algorithme à présent. Etant donné

• n le numéro de l'itération courante
• mj le score du bras j (le nombre de clic)
• nj le nombre de fois où le bras j a été joué

On choisit au temps n le bras j qui maximise la quantité suivante :

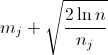
Les variantes existantes jouent sur la marge d'erreur afin d'avoir des propriétés asymptotiques les plus performantes.

3. Une ouverture vers d'autres domaines

Ces deux dernières formules sont efficaces et simples à implémenter lorsqu'on veut résoudre un problème de bandit à plusieurs bras. Aujourd'hui, l'AB testing est une forme de multi-armed bandit dans laquelle les deux bras sont les deux possibilités A et B d'un même produit. Il est bien sur possible de tenir compte des caractéristiques des visiteurs, de l'heure de la journée, du navigateur client mais le problème nécessite alors en plus des algorithmes de machine learning. Maintenir avec la même fréquence d'apparition les deux bras A et B permet de récolter plus d'information mais est sous-optimal si les produits doivent déboucher sur un processus de vente. Il convient alors d'adopter des stratégies plus fines comme celles évoquées précédemment.

4. Et les finalistes du challenge, qu'ont-t-ils fait ?

Ils sont partis sur une stratégie à trois niveaux :

1. Etant donné les problématiques de temps d’exécution d'une itération (100ms) et la probabilité qu'un passage de garbage collector fasse échouer cette itération d'une part, et d'autre part la problématique de mémoire (1,5gb ram), il a été choisi de résumer le dataset acquis progressivement par des quantiles pour les données numériques et un nombre de fixe de buckets pour les données nominales. L'autre possibilité avait été d'utiliser une fenêtre temporelle glissante mais elle aurait supposé que l'information dans le dataset soit bien répartie.
2. Le type d'algorithme choisi pour l'apprentissage une variante d'arbre de décision estimant des probabilités (dit PETs) de clic.
3. Les stratégies de combinaison des différents prédicteurs générés ont utilisé du boosting (donner plus d'importances aux bons modèles), du bagging (faire voter les différents modèles) ainsi que des agrégateurs plus spécifiques.

Les détails peuvent être trouvés dans l'article [1].

Quant à moi, je me suis efforcé d'appliquer des variantes d'UCB avec des fenêtres temporelles glissantes (la meilleure publicité peut changer avec le temps) au challenge. J'ai obtenu un score de 1475 clics bien prédits, le meilleur étant à 2170 clics, le random se situant à 1127 ± 41 clics. Sur les 500.000 visites, il y avait au plus 6678 clics à trouver.

Références :

Finite-time Analysis of the Multiarmed Bandit Problem  (un article très complet résumant de nombreux algorithmes traitant du problème du bandit à plusieurs bras)

http://explo.cs.ucl.ac.uk/ (le site du challenge n'existe plus aujourd'hui, mais des copies en cache peuvent être retrouvées)

[1] Stumping along a summary (Salperwyck and Urvoy)