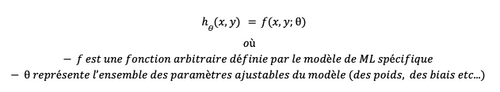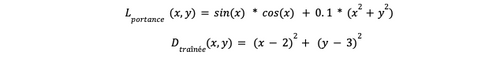[OCTO] Modélisation hybride : Quand le Machine Learning rencontre l’Optimisation.

Dans cet article, nous allons découvrir comment l’alliance de modèles de machine learning, couplés à des méthodes d’optimisation, peut répondre à des problématiques complexes issues de processus réels, qu’ils soient physiques, chimiques ou industriels.

Aujourd’hui, la recherche et l’ingénierie font face à des défis croissants : concevoir des systèmes toujours plus performants tout en réduisant les coûts, les délais et l’impact environnemental. Les processus physiques et chimiques, souvent simulés à l’aide de modèles numériques complexes ou testés en laboratoire, nécessitent des ressources considérables en calcul ou en expérimentation. Ces limites rendent difficile l’exploration exhaustive des solutions possibles (trouver la meilleure configuration ou le meilleur design possible pour le processus modélisé).

C’est ici qu’intervient la méthodologie dite de surrogate modelling optimization (ou modélisation hybride). En construisant des modèles de substitution basés sur des données, cette approche tire parti du machine learning pour remplacer ou compléter des simulations coûteuses. L’objectif ? Obtenir des approximations rapides et précises des phénomènes étudiés, tout en exploitant ces modèles dans des cadres d’optimisation pour explorer efficacement l’espace des solutions possibles.

En d’autres termes, cette méthodologie combine la puissance prédictive des algorithmes d’apprentissage automatique avec la rigueur des méthodes d’optimisation. Les applications sont variées, allant de la conception d’aéronefs à l’optimisation de procédés industriels, en passant par la recherche de matériaux innovants ou la réduction des émissions de CO₂.

Dans cet article, nous explorerons cette approche à travers un exemple, celui de la conception d’une aile d’avion. Nous verrons comment construire un modèle de substitution à l’aide de données synthétiques, l’entraîner avec des outils comme Python et Keras, et l’utiliser pour résoudre un problème d’optimisation. Cet article nous permettra de comprendre les principes fondamentaux et les subtilités de cette méthodologie, qui s’impose comme un outil incontournable dans de nombreux domaines d’ingénierie.

1. Exemple de “Surrogate Modelling Optimization”

Contexte

Prenons un problème d’optimisation classique dans lequel nous avons une fonction objectif f(x,y) que nous souhaitons maximiser (ou minimiser) en fonction de paramètres x, y, soumis à des contraintes de valeurs minimales et maximales :

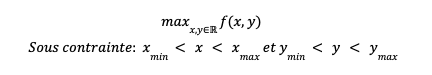
Maintenant, imaginons que vous soyez une équipe d’ingénieur(e)s aéronautiques, et que vous travaillez sur la conception d’une nouvelle aile pour un des futurs avions fabriqués par votre société.

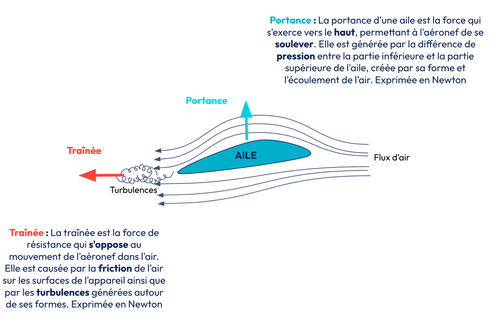
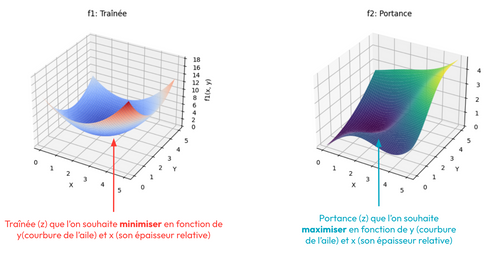
Dans ce contexte, la fonction f pourrait correspondre à la valeur de la portance d’une aile d’avion en fonction de sa courbure, représentée par x et de son épaisseur relative y. Une aile d’avion a plusieurs propriétés qui découlent de sa forme. Nous avons déjà la portance, mais lorsque nous faisons varier les paramètres x et y, cela impacte une autre propriété : la traînée. La portance améliore la capacité de charge et détermine la longueur minimale de la piste de décollage par exemple. Nous souhaitons la maximiser. À l’inverse, la traînée impacte la consommation de carburant et nous voulons donc la minimiser [4].

Figure 1. Traînée et Portance d’une aile d’avion.

Formalisons ce problème d’optimisation :

“Nous souhaitons trouver les valeurs optimales de la courbure y et l’épaisseur relative x d’une aile d’avions, maximisant sa portance, Lportance et minimisant la Dtraînée, x et y devant être dans une plage de valeurs acceptables”

Ce problème d’optimisation traduit précisément notre objectif métier : concevoir une aile optimale en maximisant la portance et en minimisant la traînée tout en respectant les contraintes imposées. Cependant, nous n’avons pas encore introduit la modélisation par machine learning, qui interviendra dans la suite pour résoudre ce problème efficacement.

Besoin d’approximation

Les effets de x et y sur la portance et la traînée sont déterminés par les lois de la physique. Nous n’avons pas de formule mathématique nous permettant, à partir des caractéristiques d’une aile, de nous donner sa traînée et sa portance. Pour obtenir ces valeurs, nous avons deux possibilités : entrer ces valeurs dans un simulateur pour obtenir la portance et la traînée, ou réaliser une maquette avec des capteurs et la passer dans une soufflerie. Pour des raisons de coût et de temps, la seconde option est réservée pour le cas où la conception est déjà bien avancée.

La solution du simulateur de soufflerie est intéressante, elle permet, pour une configuration donnée de x et y , en quelques dizaines de minutes de calcul de simulation de mécanique des fluides, sur des supercalculateurs, d’obtenir la portance et la traînée de l’aile. Néanmoins, avec le nombre de combinaisons possibles de x et y, on se rend compte qu’il va être difficile trouver la solution optimale à notre problème : le nombre configurations explorées et testées est limité par le temps de calcul et le temps d’occupation du supercalculateur.

Et c’est là qu’intervient le surrogate modelling, ou modèle de substitution. Dans un modèle ML général, la fonction d'hypothèse h peut être représentée par une fonction paramétrique non linéaire :

Un modèle de machine learning va être entraîné afin que h(x,y) soit aussi proche que possible de la fonction cible f(x,y)

Cette fonction cible pourrait par exemple être Lportance(x,y) ou Dtraînée(x,y)

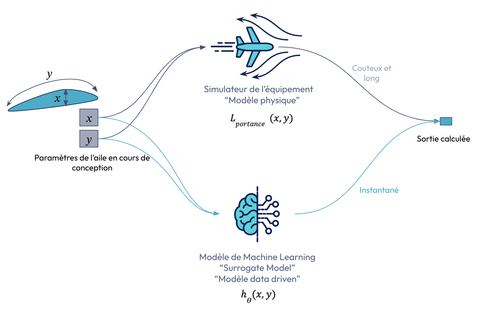
Figure 2. Illustration de l’intégration du surrogate modelling dans notre cas concret

Ainsi, nous venons de faire le lien entre la partie optimisation vue plus haut, et la partie Machine learning. Pour résumer, le machine learning va venir se substituer aux simulations qui sont coûteuses en moyens et en temps. Une inférence d’un modèle de machine learning prend généralement une fraction de seconde, là où l’obtention d’un résultat via une simulation peut prendre plusieurs minutes, voire des heures.

Applications

Le fil rouge de notre article va être cet exemple de conception (très simplifié) d’aile d’avion. Mais il existe une multitude de cas d’applications de cette méthodologie dans le monde réel : optimisation de processus chimiques ou physiques, design de matériaux. Parmi les exemples trouvés dans la littérature, voici ceux qui ont attiré notre attention :

• Optimisation de la captation de co2 [10]
• Optimisation de la production d’hydrogène avec un “auto thermal reformer” [11]
• Optimisation du design d’une batterie [12]
• Optimisation de la conception de matériaux de protection thermique

On pourrait se risquer à généraliser : dès que vous avez un processus physique/chimique que vous souhaitez optimiser et que le modèle (simulateur ou physique) a un coût d’inférence élevé, il est possible que l’utilisation de modélisation hybride soit une solution.

2. Un exemple avec Python

Nous vous proposons de dérouler en Python, un cas d’application de la modélisation hybride. Nous commencerons par l’acquisition des données nécessaires à l’entraînement du modèle de machine learning. Nous entrainerons le modèle de machine learning et discuterons de certains points d’attention et enfin, nous utiliserons ce modèle pour trouver la configuration optimale de l’aile.

Les données d'entraînement

L’apprentissage d’un modèle de machine learning nécessite d’avoir des données, et de préférence en grande quantité. Dans l’introduction, nous avons vu que la méthode d’optimisation que nous sommes en train d’étudier pouvait être appelée “data driven optimization”. Les données utilisées peuvent provenir de plusieurs sources :

• Si vous disposez d’un simulateur suffisamment précis du processus que vous souhaitez optimiser, vous pouvez l’utiliser pour générer des données d’apprentissage. Ceci peut être long et coûteux. Dans ce cas, il faudra mettre en place une méthode d’échantillonnage qui vous permettra d’obtenir une bonne représentativité de votre espace de modélisation en un minimum de points. Si vous disposez d’un historique des simulations ou des expérimentations passées, vous pouvez le compléter avec cet échantillonnage.
• S’il s’agit d’un processus réel qui fonctionne en continu (processus industriel, chimique par exemple) et pour lequel vous avez des données de suivi historiques (capteurs, conditions environnementales, configurations), vous pourrez les utiliser pour modéliser votre processus.

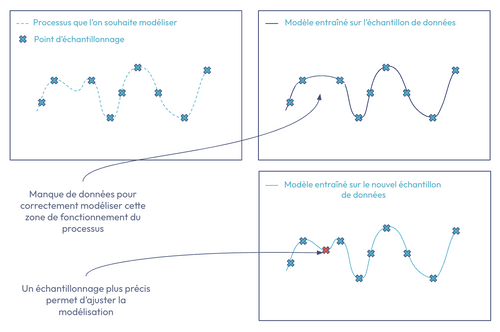
La figure ci-dessous nous rappelle l’importance d’avoir un jeu de données représentatif du processus que l’on souhaite modéliser. Dans le cas contraire, le modèle appris renverra des valeurs ne correspondant pas à la réalité. Dans notre optimisation, cela pourrait se traduire par des recommandations de valeur optimales fausses.

Figure 3. Apprentissage d’un modèle de ML avec des données insuffisantes

Données synthétiques

L’objectif de cet article n’étant pas de designer une aile d’avion réaliste, mais d’expliquer comment fonctionne l’hybridation de modèles de ML et d’optimisation, nous proposons d’utiliser des données synthétiques générées à partir de fonctions ayant des propriétés adéquates pour cet exemple.

Pour représenter nos deux fonctions Lportance(x,y) et Dtraînée(x,y) nous utiliserons deux fonctions :

Encore une fois, ces fonctions ne sont pas du tout issues de la dynamique des fluides et servent juste d’exemple pour notre optimisation.

Visualisons ces fonctions en 3D dans un notebook Python :

Figure 4. Visualisation de nos fonctions synthétiques symbolisant la Traînée et la Portance

Nous allons utiliser ces fonctions pour générer quelques milliers de points qui nous serviront de base de données d’apprentissage.

3 Entraînement du modèle

Nous allons utiliser keras pour entraîner un modèle qui prédit la portance et la traînée. Les réseaux de neurones peuvent avoir plusieurs sorties. Dans notre cas, nous utiliserons un réseau de neurones multicouche utilisant des fonctions d’activation sigmoïde. Ce réseau de neurones sera le modèle de substitution pour notre aile. Il prendra en entrée x et y et prédira la portance et la traînée.

Il est possible d’utiliser d’autres types de modèles, la seule condition est qu’il soit convertible en fonction objectif pour un problème d’optimisation. Nous en reparlerons plus loin.

Commençons par créer un perceptron multicouche :

• Deux entrés (x et y)
• Une couche cachée de 64 neurones à activation sigmoïde
• Une couche cachée de 32 neurones à activation sigmoïde
• Deux sorties (L et D)

Il devrait suffire à prédire correctement nos fonctions synthétiques.

Le code ci-dessous montre la construction du réseau de neurones en Keras, son entraînement sur un jeu de données d’apprentissage et la validation sur les données de test. Nous ne nous attarderons pas sur la partie apprentissage dans cet article.

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_percentage_error
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import pandas as pd

data = pd.read_parquet('../data/data.parquet')

features = data[["x", "y"]]
targets = data[["f1", "f2"]]

X_train, X_test, y_train, y_test = train_test_split(features, targets, test_size=0.2)

# Créer le modèle PMC
model = Sequential([
    Dense(32, input_dim=2, activation='sigmoid'),  # Couche cachée de 32 neurones
    Dense(32, activation='sigmoid'),  # Couche cachée de 32 neurones
    Dense(2)  # Couche de sortie avec 2 neurones (pour f1 et f2)
])

model.compile(optimizer='adam', loss='mse', metrics=['mae'])

history = model.fit(X_train, y_train, epochs=200, validation_data=(X_test, y_test),batch_size=8)

model.save("plane_nn_sigmoid.keras")

Nous pouvons vérifier que nous avons les performances en qualité de prédiction :

# Évaluer le modèle
loss, mae = model.evaluate(X_test, y_test)
y_test_pred = model.predict(X_test)
mape = mean_absolute_percentage_error(y_test, y_test_pred)
print(f'Loss: {loss}, MAE: {mae}, MAPE: {mape}')

Loss: 0.008396115154027939, MAE: 0.06722036004066467, MAPE: 0.08936714849698064

Nous avons une erreur en pourcentage moyenne de 8%, ce qui suffira pour notre article.

Enfin, vu que nous travaillons sur des données synthétiques en 3D, nous pouvons visualiser les fonctions apprises par le modèle en générant une grille de points et en les affichant. Nous faisons cela à titre purement pédagogique. Les processus que nous modélisons dans la vie réelle le sont rarement en moins de 3 dimensions.

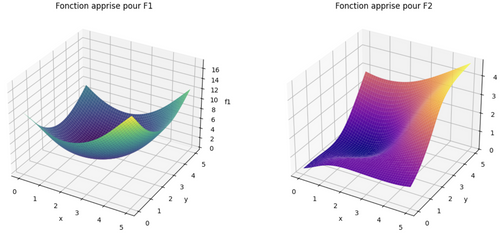
Figure 5. Visualisation des fonctions apprises par notre modèle Keras, pour la traînée et la portance

Nous sommes satisfaits du modèle appris. Il représente fidèlement le processus (fictif) que nous souhaitons modéliser. Nous pouvons passer à la partie optimisation !

4. Définition du problème d’optimisation

A. Pyomo : librairie d’optimisation en Python

Pour résoudre notre problème d’optimisation, nous allons utiliser une librairie très populaire : Pyomo. Cette librairie permet de formaliser des problèmes d’optimisation en python et d’utiliser différents solver (gratuits ou payants) pour les résoudre.

Nous n’allons pas rentrer dans le détail des fonctionnalités proposées par Pyomo, mais regardons tout de même son fonctionnement sur un exemple facile d’optimisation.

Imaginons un problème simple :

Une entreprise fabrique deux produits, P1​ et P2. Chaque produit a un coût de production et un prix de vente. L'objectif est de maximiser le profit tout en respectant les contraintes de production.

Données :

• Le produit P1​ génère un bénéfice de 40 € par unité.
• Le produit P2 génère un bénéfice de 30 € par unité.
• Le produit P1​ nécessite 2 heures de travail et 3 kg de matière première par unité.
• Le produit P2 nécessite 4 heures de travail et 2 kg de matière première par unité.
• Il y a un total de 100 heures de travail disponibles.
• Il y a 120 kg de matière première disponibles.

Ce problème se formalise de la façon suivante :

Ce problème se traduit en Pyomo de la manière suivante :

import pyomo.environ as pyo

# Modèle Pyomo
model = pyo.ConcreteModel()

# Variables
model.x1 = pyo.Var(domain=pyo.NonNegativeIntegers)  # Quantité de P1 
model.x2 = pyo.Var(domain=pyo.NonNegativeIntegers)  # Quantité de P2

# Paramètres
profit_P1 = 40
profit_P2 = 30
work_limit = 100
material_limit = 120

# Fonction objectif : Maximiser le profit
# Expr contient la formalisation de la fonction objectif. p1 x x1 + p2 x x2 
model.profit = pyo.Objective(expr=profit_P1 * model.x1 + profit_P2 * model.x2, sense=pyo.maximize)

# Contraintes
# Limite de temps de travail total disponible
model.work_constraint = pyo.Constraint(expr=2 * model.x1 + 4 * model.x2 <= work_limit)
# Limite de matériau disponible
model.material_constraint = pyo.Constraint(expr=3 * model.x1 + 2 * model.x2 <= material_limit)

# Résolution
# Ici, on précise le solver que l'on souhaite utiliser
solver = pyo.SolverFactory('cbc')  # Vous pouvez utiliser 'cbc', 'gurobi', etc.
result = solver.solve(model)

# On affiche les résultats
print("Status:", result.solver.termination_condition)
print("Quantité optimale de P1:", model.x1())
print("Quantité optimale de P2:", model.x2())
print("Profit maximal:", model.profit())

L’exécution de ce code nous donne le résultat suivant :

• La quantité optimale de produit de type P1 est 36.
• La quantité optimale de produit de type P2 est 6
• Le profit obtenu avec ces quantités est de 1620.

Maintenant que nous avons vu comme définir un problème classique d’optimisation en Pyomo, voyons comment nous pouvons intégrer notre modèle de Machine learning en tant que fonction objectif.

B.OMLT: formulation d’un modèle de machine learning en fonction objectif

OMLT (Optimization & Machine Learning Toolkit) est une bibliothèque Python conçue pour intégrer de manière transparente des modèles de machine learning dans des cadres d’optimisation mathématique. Développée pour répondre aux besoins des chercheurs et des ingénieurs, elle permet de convertir des modèles prédictifs entraînés avec des outils populaires comme TensorFlow, PyTorch ou Keras en formulations mathématiques exploitables par des solveurs d’optimisation. Cela inclut la conversion de réseaux de neurones, de forêts, d’arbres de décision ou d’autres modèles paramétriques en représentations linéaires, quadratiques ou non linéaires adaptées aux solveurs comme Gurobi, CPLEX ou IPOPT.

En pratique, OMLT permet d’utiliser un modèle de machine learning comme une fonction objectif ou une contrainte dans un problème d’optimisation. Par exemple, un réseau de neurones prédisant une valeur physique (comme la portance ou la traînée d’une aile d’avion) peut être directement intégré dans un problème où l’objectif est de maximiser une performance ou minimiser un coût. La bibliothèque offre également des outils pour simplifier les modèles complexes et améliorer leur compatibilité avec les solveurs, comme l’approximation des fonctions non linéaires par des modèles mixtes entiers linéaires (MILP).

Grâce à OMLT, il devient possible de combiner la puissance des modèles d’apprentissage automatique avec la précision et la rigueur des techniques d’optimisation. Nous allons utiliser cette librairie pour résoudre notre problème.

C. Rappel sur l’inférence d’un réseau de neurones

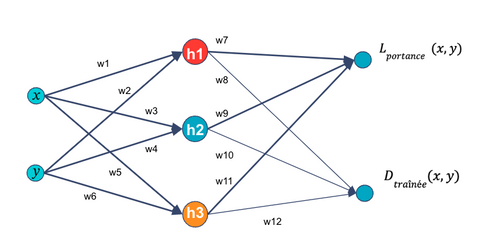
Effectuons tout d’abord un petit rappel sur l’inférence d’un perceptron multicouche. Voici un schéma d’un réseau de neurones simplifié avec une seule couche cachée de 3 neurones.

Figure 6. Schéma d’un perceptron multicouche

La formule suivante nous donne le calcul qui permet, à partir de x et y et du modèle, d’arriver aux valeurs de sortie Lportance(x,y) :

C’est cette formule que OMLT construit et définit comme fonction objectif dans Pyomo (framework d’optimisation Python). Dans notre cas, nous utilisons une formulation FullSpaceSmoothNN. La formule sera utilisée telle quelle sans approximation linéaire. Ceci implique donc d’utiliser un solver capable de résoudre des problèmes non linéaires, car la fonction d’activation sigmoïde est non linéaire.

5. Résolution du problème avec Pyomo et OMLT

Définissons maintenant notre modèle d’optimisation d’une aile en Pyomo. La première étape va être de charger notre modèle Keras et de le transformer en expression Pyomo grâce à OMLT.

from omlt.neuralnet import FullSpaceSmoothNNFormulation

# Charger le modèle Keras
nn= tensorflow.keras.models.load_model("plane_nn_sigmoid.keras", compile=False)
net = load_keras_sequential(nn, unscaled_input_bounds={0: (0,5 ), 1: (0,5 )})

# 2. Définir le modèle Pyomo pour l'optimisation
pyomo_model = pyo.ConcreteModel()

# Ajouter un bloc OMLT pour intégrer le réseau de neurones
pyomo_model.neural_network = OmltBlock()

# Transformer notre réseau de neurones en formulation Omlt pour l'utiliser comme expression Pyomo
formulation = FullSpaceSmoothNNFormulation(net)
pyomo_model.neural_network.build_formulation(formulation)

Nous pouvons remarquer que le début de la modélisation est similaire à celui du problème vu dans 4.A.

Nous instancions à modèle Pyomo : pyomo_model. A ce modèle est ajouté un bloc OMLT qui sera l’attribut “neural_network” de notre modèle Pyomo.

Dans la suite du code, nous indiquons que la fonction objectif (pyomo.objective) à maximiser (pyo.maximize) est la différence entre la portance (deuxième sortie du réseau de neurones) et la traînée (première sortie du réseau de neurones).

# Première sortie du réseau de neurones : la traînée
f1 = pyomo_model.neural_network.outputs[0]
# Deuxième sortie du réseau de neurones : la portance
f2 = pyomo_model.neural_network.outputs[1]

# 3. Formuler l'objectif de maximisation de f1 - f2
pyomo_model.objective = pyo.Objective(expr=f2 - f1, sense=pyo.maximize)

Dans la formulation de notre problème, nous indiquons que x et y doivent être supérieurs à 0. (L’épaisseur d’une aile et sa courbure ne peuvent pas être nulles ou négatives).

# 4. Ajouter des contraintes sur les valeurs de x et y
pyomo_model.con_x = pyo.Constraint(expr=pyomo_model.neural_network.inputs[0] >= 0)
pyomo_model.con_y = pyo.Constraint(expr=pyomo_model.neural_network.inputs[1] >= 0)

Le problème est prêt à être résolu ! Nous utiliserons le solver ipopt qui est un solver capable de gérer des problèmes non linéaires (la fonction sigmoïde est non linéaire).

solver = pyo.SolverFactory("ipopt")
status = solver.solve(pyomo_model, tee=False)

Il ne reste plus qu’à afficher les résultats. Les valeurs de variables d’un modèle Pyomo se récupèrent grâce à la fonction “value”.

# 5. Afficher les résultats optimaux
optimal_x = pyo.value(pyomo_model.neural_network.inputs[0])
optimal_y = pyo.value(pyomo_model.neural_network.inputs[1])
optimal_f1 = pyo.value(f1)
optimal_f2 = pyo.value(f2)
optimal_value = optimal_f2 + optimal_f1

print(f'Valeurs optimales : x = {optimal_x}, y = {optimal_y}')
print(f'f1 = {optimal_f1}, f2 = {optimal_f2}')
print(f'Valeur de f1 - f2 maximale : {optimal_value}')

L’exécution de ce notebook python nous donne les résultats suivants :

Nous venons de résoudre en quelques lignes de code un problème d’optimisation intégrant un modèle de machine learning dans sa formulation !

6. Et dans la vraie vie ?

Je déconseille fortement d’essayer de concevoir un véritable avion en utilisant les valeurs présentées dans cet article, car les données employées ici sont purement synthétiques. Ce problème simplifié s’inspire cependant de cas réels, [3][5][6], où la conception d’aéronefs, de processus industriels ou de matériaux exige des modèles bien plus sophistiqués et des données issues de simulations précises ou d’expériences en laboratoire.

L’objectif de cet article était avant tout de démontrer que l’alliance du Machine Learning et de la recherche opérationnelle est non seulement possible, mais aussi rendue accessible grâce à des outils comme Pyomo ou OMLT. Ces librairies permettent d’intégrer efficacement des modèles de substitution dans des cadres d’optimisation, ouvrant ainsi la porte à de nouvelles applications dans des domaines variés.

Prenons l’exemple officiel d’OMLT [11] sur l’optimisation d’un auto thermal reformer : cette technologie illustre parfaitement l’intérêt de ces outils pour modéliser et optimiser des processus industriels chimiques complexes. Souvent, ces systèmes requièrent l’utilisation de plusieurs modèles de substitution interconnectés, un défi que Pyomo et OMLT peuvent relever avec flexibilité.

Enfin, il est également courant d’exploiter les sorties d’un modèle de machine learning comme des contraintes dans un problème d’optimisation. Par exemple, nous aurions pu transformer notre exemple en maximisant la portance sous la contrainte d’un poids de l’aile limité, ce poids étant calculé par un modèle prenant en compte les dimensions (x, y) et les propriétés des matériaux utilisés.

Le repository de code avec les notebooks et les données utilisées est accessible ici :

https://github.com/philippestepniewskiperso/surrogate_optimization_plane

Références :

[1] Cog-Imperial. (s. d.). GitHub - cog-imperial/OMLT : Represent trained machine learning models as Pyomo optimization formulations. GitHub. https://github.com/cog-imperial/OMLT

[2] Pyomo. (s. d.-a). GitHub - Pyomo/pyomo : An object-oriented algebraic modeling language in Python for structured optimization problems. GitHub. https://github.com/Pyomo/pyomo

[3] Thirumalainambi, R., & Bardina, J. (2003). Training data requirement for a neural network to predict aerodynamic coefficients. Proceedings Of SPIE, The International Society For Optical Engineering/Proceedings Of SPIE. https://doi.org/10.1117/12.486343

[4] Contributeurs aux projets Wikimedia. (2024, 9 novembre). Portance (aérodynamique). https://fr.wikipedia.org/wiki/Portance_(a%C3%A9rodynamique)

[5] López, R. (2024, 19 février). Predict airfoil self-noise using machine learning. Neural Designer. https://www.neuraldesigner.com/learning/examples/airfoil-self-noise-prediction/

[6] López, R. (2023, 13 novembre). Performance optimization using machine learning. Neural Designer. https://www.neuraldesigner.com/solutions/performance-optimization/

[7] Schweidtmann, A. M., Esche, E., Fischer, A., Kloft, M., Repke, J., Sager, S., & Mitsos, A. (2021). Machine Learning in Chemical Engineering : A Perspective. Chemie Ingenieur Technik, 93(12), 2029‑2039. https://doi.org/10.1002/cite.202100083

[8] Surrogate Models - Gurobi Machine Learning Manual. (s. d.). https://gurobi-machinelearning.readthedocs.io/en/stable/auto_examples/example1_2DPeakFunction.html

[9] Gorissen, Dirk & Dhaene, Tom & Co, Dhaene & Suykens, Johan & Bultheel, Adhemar. HETEROGENEOUS EVOLUTION OF SURROGATE MODELS. https://www.researchgate.net/publication/355490376_Machine_Learning_in_Chemical_Engineering_A_Perspective

[10] Xing, Lei & Jiang, Hai & Wang, Shuo & Pinfield, Valerie & Xuan, Jin. (2022). Data-driven surrogate modelling and multi-variable optimization of trickle bed and packed bubble column reactors for CO2 capture via enhanced weathering. Chemical Engineering Journal. 454. 139997. 10.1016/j.cej.2022.139997.

[11] Autothermal Reformer Flowsheet Optimization with OMLT (TensorFlow Keras) Surrogate Object — IDAES Examples. (s. d.). https://idaes-examples.readthedocs.io/en/2.5.0/docs/surrogates/omlt/keras_flowsheet_optimization_doc.html

[12] Amiri, Mahshid N. & Håkansson, Anne & Burheim, Odne S. & Lamb, Jacob J., 2024. "Lithium-ion battery digitalization: Combining physics-based models and machine learning," Renewable and Sustainable Energy Reviews, Elsevier, vol. 200(C).