[OCTO] Article de Blog - SICA/VIVA Données synthétiques

Quand la génération synthétique permet de voir ce qui n’existe pas

Cet article s’appuie sur un cas d’usage industriel concret, la détection automatique de défauts sur des soudures métalliques. Dans ce type de procédé, un faisceau électrique ou laser vient fondre deux pièces pour les assembler, créant un cordon de soudure dont la qualité dépend de nombreux facteurs comme la tension du courant ou encore les conditions d’éclairage pendant la capture. Ainsi, la moindre variation de vitesse ou de surface peut rapidement créer un défaut.
Mais ces défauts, rares par nature, posent un vrai défi : comment entraîner un modèle d’IA à les reconnaître quand la production n’en génère presque jamais ?

C’est là que la donnée synthétique entre en jeu.

En générant de manière contrôlée des défauts plausibles sans perturber la production, elle permet d’élargir la vision du modèle et de renforcer sa fiabilité.
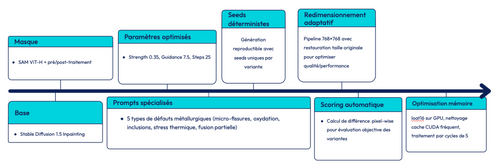
L’article explore ce principe à travers un pipeline mêlant segmentation automatique, génération guidée et validation expérimentale, pour comprendre comment le faux utile peut rendre l’IA industrielle plus juste, plus robuste et, paradoxalement, plus proche du réel.

0. Le point de départ

En illustration de cet article, l’analyse s'appuie sur des expérimentations réalisées sur un système de détection de défauts de soudure. Les exemples et résultats proviennent de ce cas d’usage réel.

En industrie, les défauts graves sont rares par définition. Quand un processus de production atteint un haut niveau de maturité, il devient trop efficace pour apprendre de ses erreurs. Les modèles de détection d’anomalies subissent une contradiction, celle de devoir reconnaître des événements qu’ils ne voient presque jamais.

Mathématiquement, le modèle va chercher à approximer la distribution conditionnelle suivante :

P(X|Y = KO)

où X représente les images de soudures, Y leur étiquette (OK ou KO ) et P étant la distribution de X observée en usine.

On peut alors se demander comment enrichir cette distribution pour couvrir les multiples formes de défauts possibles, sans inventer des anomalies physiquement absurdes. Autrement dit, comment étendre la couverture du réel sans trahir la physique du procédé industriel ?

Le vrai problème ne vient pas vraiment du modèle lui-même, mais plutôt de ce qu’on lui donne comme matière d’apprentissage. Et c’est justement là que la donnée synthétique peut s’avérer utile et prendre un réel sens, en permettant de réinventer le réel sans jamais le trahir.

1. Quand le réel devient un luxe

Dans l’industrie, chaque donnée collectée a un prix. En effet, une simple image n’est jamais anodine : elle implique un contrôle qualité, parfois un arrêt de la ligne de production et l’intervention d’un qualiticien pour l’annoter.

Les vrais défauts sont rares (fissures, porosités, soudures oxydées…). En effet, à peine 1 à 2 % des pièces sont défectueuses, parfois moins encore. Et quand on en trouve, ces défauts sont souvent assez proches, prise de vue similaire, mêmes angles, mêmes caméras, mêmes conditions de lumière. Le résultat est que l’on se retrouve avec une base d’images plutôt uniforme.

Les modèles deviennent excellents sur leur terrain d’origine, mais incapables de s’adapter à d’autres contextes. Ce n’est pas une question de quantité mais davantage de représentativité. Plus la production est maîtrisée, moins elle offre de situations dont on peut apprendre. Plus l’usine fabrique bien, moins l’IA peut comprendre ce qu’est un défaut.

La qualité industrielle, en éliminant les anomalies, finit par priver l’apprentissage automatique de la matière première dont il a besoin. Le réel en devient presque un luxe.

Il faut alors redoubler d’imagination pour trouver des moyens sûrs et maîtrisés d’en recréer les marges et de simuler ces écarts, qui permettent au modèle d’apprendre.

Quand l'œil humain lui-même hésite

Pour saisir toute la difficulté du problème, observons deux soudures :

              Soudure OK vs Soudure KO

À gauche, une soudure conforme. À droite, une autre presque identique. Et pourtant ce sont ces micromètres de différences qui peuvent provoquer une rupture mécanique. C’est précisément dans ces zones d’incertitude que le modèle doit être le plus fiable et pressentir les anomalies. Or ces situations, ces « presque défauts », sont aussi les cas les plus rares car difficiles à repérer et souvent uniques.

2. Le paradoxe du faux utile

Et si, pour mieux comprendre le réel, il fallait commencer à le simuler ?

La donnée synthétique, générée artificiellement, n’est ni “vraie” ni “fausse” au sens classique. D’abord elle n’est pas vraie puisqu’aucun capteur ne l’a observée, mais elle n’est pas fausse pour autant si elle aide un modèle à mieux apprendre la vérité du terrain.

Mathématiquement, nous cherchons à créer une distribution générative Q(X|Y = KO) telle que :

Q(X|Y = KO) ≈ P(X|Y = KO)

Le symbole “≈” rappelle qu’il n’est pas possible de reproduire à 100 % la réalité. Dans la pratique, la distribution générative est implémentée par Stable Diffusion (SD), un modèle de diffusion latent qui génère les images synthétiques. À l’inverse, P désigne la vraie distribution observée en usine. Tout l’enjeu du pipeline est de réduire l’écart entre ces deux distributions.

Finalement, on cherche à produire des échantillons synthétiques x*′* qui se comportent, pour le modèle, comme de vrais cas x de P. Ce qu’il faut saisir, c’est que l’enjeu n’est donc pas esthétique (obtenir de “belles” images), mais épistémique.

Épistémique : relatif à la connaissance et à ses conditions de validité. Une question épistémique porte sur "comment sait-on ce qu'on sait ?"

L’objectif premier est de fabriquer des échantillons plausibles et utiles. Concrètement, on veut que ces images améliorent la frontière de décision du modèle entre OK et KO.

Cette ligne est fine, car si l’on commence à générer des images avec un modèle déjà entraîné sur des données synthétiques, puis à réentraîner de nouveaux modèles sur ces images générées, on crée une boucle d’autoréférence. À chaque itération, un modèle apprend surtout à être bon sur des données qu’un autre modèle a inventées. Le risque est alors que le faux finisse par valider le faux. Les performances restent élevées sur les images générées, mais se dégradent sur les vraies images de terrain.

Durant tout le processus, il faut donc mettre en place un contrôle épistémique, une sorte de cadre définissant à quelles conditions une donnée synthétique est légitime.

Les fondements informationnels du faux utile

Si la donnée synthétique peut vraiment aider, c’est parce qu’elle rééquilibre l’information dans l’espace d’apprentissage. En théorie de l'information, on dit qu’une observation x est informative quand elle est rare. Sa valeur informationnelle est donnée par :

I(x) = -logP(x)

Cette formule introduite par Claude Shannon dans sa théorie de l’information (1948) explique que l'information est inversement proportionnelle à la probabilité (C.E. Shannon (1948). "A Mathematical Theory of Communication")

Elle soulève une intuition, celle que plus un événement est improbable, plus il est riche d’enseignement. Si on sort la calculette, une soudure dite normale (par exemple P = 0.98 ) apporte I = -log(0.98) = 0.03 bit d’information. Un défaut (disons par exemple P = 0.02 ) va apporter I = -log(0.02) = 5.6 bits. Un défaut contient donc presque 200 fois plus d’informations qu’une soudure normale (nous sommes en base 2 ici).

Or les défauts industriels (Y = KO) sont précisément ces événements à forte information car ils se produisent peu mais disent beaucoup. Le problème c’est que notre dataset réel les capture mal. Il représente très bien les cas normaux, mais très peu les zones où l’usine déraille. Ainsi, pendant l’entraînement, le modèle apprend surtout ce qu’il voit souvent et reste un peu aveugle à la rareté.

La donnée synthétique vient corriger cette cécité. Elle va ajouter des exemples plausibles de KO qui va augmenter ce qu’on pourrait appeler l’entropie utile du jeu d’apprentissage :

H_eff = H(Préel) + ΔHsynth

où :

• H*_eff* est l’entropie effective totale du dataset enrichi
• H(Préel) est l’entropie du dataset réel d’origine
• ΔHsynth représente l’entropie ajoutée par la génération synthétique

ΔHsynth représente l'entropie ajoutée par la génération artificielle. Cette entropie supplémentaire est un désordre contrôlé qui est ajouté dans les zones du réel où l’on manque de diversité. Le but n’est pas de rendre les images plus variées visuellement, mais de couvrir davantage de configurations (formes de fissure, motifs de porosité, types d’oxydation) que le modèle doit reconnaître. Si ΔH devient trop grand (génération trop variée), on sort du domaine industriel plausible. On a un équilibre quand H*_eff* augmente, mais il doit rester cohérent avec ce que la physique autorise.

3. Fabriquer le plausible, pas l’illusion du plausible

Architecture du pipeline de génération

3.1. Définir ce qu’on choisit de voir

Tout commence par la délimitation du champ d’apprentissage.
On isole automatiquement la zone de soudure à l’aide de SAM (Segment Anything Model), développé par Meta AI (Kirillov 2023)

SAM est distribué sous une licence open source permissive Apache 2.0, ce qui permet son intégration libre dans des pipelines industriels. C’est un modèle entraîné en zero-shot sur des millions d’images qui produit plusieurs dizaines de masques candidats par image. Un score composite sélectionne celui qui correspond à la géométrie du cordon :

S_mask = w₁ * ratio(L/H) + w₂* contraste + w₃* variance interne + w₄* centrage

Cette formule articule 4 métriques physiques : le ratio longueur/hauteur (forme allongée du cordon), le contraste (capacité de distinction du fond), l'homogénéité de texture et le centrage dans l'image.

Les coefficients empiriques (w₁ = 0.35, w₂ = 0.30, w₃ = 0.20, w₄ = 0.15 ) normalisent le score. Seuls les masques ayant S_mask > 0.65 sont conservés.

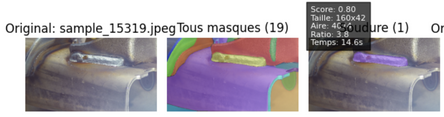
Exemples de segmentations automatiques du cordon de soudure avec SAM (mask en rose)

3.2. Inpainting

Le pipeline utilise Stable Diffusion v1.5 Inpainting, un modèle de diffusion capable de générer ou modifier une image à partir d’un prompt, tout en se basant sur une image de référence et un masque indiquant les zones à retravailler.

Ce choix s’explique car le modèle préserve le contexte physique avec un contrôle précis et une empreinte mémoire légère. Les alternatives plus complexes (ControlNet mlsd et LoRA) se sont révélées instables, génératrices d’artefacts et trop lourdes (environ 14 Go VRAM), donc peu adaptées à un usage industriel.

Inpainting : technique consistant à remplir ou modifier une zone masquée d'une image de manière cohérente avec le reste.

Contrairement aux GAN qui apprennent une transformation directe bruit → image, Stable Diffusion fonctionne par débruitage itératif. Durant l'entraînement, on ajoute progressivement du bruit gaussien à une image réelle sur un certain nombre d’étapes. Le modèle apprend ensuite à faire le chemin inverse, en retirant le bruit étape par étape pour reconstruire une image réaliste. Ce principe est appliqué sur un espace latent compressé (64×64×4 au lieu de 512×512×3), ce qui accélère le calcul et permet de guider la génération avec du texte (encodeur CLIP) et un masque.

Concrètement, on construit un masque M de même taille que l’image x. Ce masque vaut 1 sur les pixels du cordon de soudure que l’on souhaite éditer, et 0 sur le reste de l’image. Seule cette zone masquée est donc modifiée par le modèle :

x’ = ( 1 - M ) ⊙ x + M ⊙ f_θ(x, M, p)

Ici x’ est la composition de l'image finale, f_θ est le modèle de diffusion guidé par le contexte x, le masque M, et le prompt p (par exemple "fine crack", "oxidized weld").

Le modèle de diffusion utilise trois hyperparamètres classiques pour l’inpainting. La strength est fixée à 0.35, elle contrôle le taux d’édition, donc la proportion de l’image initiale qui sera rééchantillonnée. Sa valeur théorique varie entre 0 et 1, et l’on opère généralement entre 0.2 et 0.6. Avec 0.35, on conserve la structure réelle de la soudure tout en introduisant un défaut clairement visible. Le guidance_scale est fixé à 7.5. Ce paramètre détermine le poids du prompt textuel relativement à l’image d’entrée. Les valeurs usuelles tournent autour de 7. Enfin, le nombre de steps est fixé à 25, ce qui correspond au nombre d’itérations de débruitage. Plus il est élevé, plus la génération est précise mais coûteuse, les valeurs typiques se situent entre 20 et 50. Se limiter à 25 offre un compromis satisfaisant entre qualité de génération, cohérence physique et performance.

Exemples de défauts synthétiques générés par inpainting avec Stable Diffusion. À gauche : image réelle de référence. À droite : image synthétique avec défaut ajouté.

3.3. Scoring S_i pour juger la crédibilité du faux

Chaque image synthétique reçoit un score de crédibilité :

S_i = λ₁ R_i + λ₂U_i

où R*~i ~ est le réalisme visuel (cohérence texture) et U_i* l'utilité ML (la diversité sémantique). Seules les images avec S_i > 0.7 sont conservées.

3.4. Déduplication et gouvernance (POOL★)

Chaque image est encodée par un embedding CLIP, et la similarité cosinus est calculée de la façon suivante :

sim(e_i, e_j) =〈 e_i , e_j 〉/ ‖e_i ‖ ‖e_j ‖

Cette formule calcule la similarité cosinus entre deux vecteurs d’embedding e*_i* et e*_j* (de dimension 512 chacun). Elle mesure l’angle entre ces deux vecteurs : plus ils pointent dans la même direction, plus les images sont similaires.

La division par les normes sert à normaliser les vecteurs, on compare donc uniquement leur orientation, pas leur magnitude. Géométriquement :

• θ = 0° → cos = 1 → similarité = 1 : images quasi identiques
• θ = 90° → cos = 0 → similarité = 0 : images sans relation

Dans le pipeline, deux images sont considérées comme doublons (et fusionnées) lorsque leur similarité dépasse 0.995.

L’ensemble final constitue le POOL★ (la bibliothèque de données synthétiques validées), une base qui est versionnée et qui contient les prompts, les seeds, les masques utilisés, les scores S*_i​* ainsi que les versions de modèle.

Workflow de filtrage et de sampling. Le ratio réel-synthétique est ajusté dynamiquement selon les performances observées, avec un seuil optimal identifié à 15% de synthétique

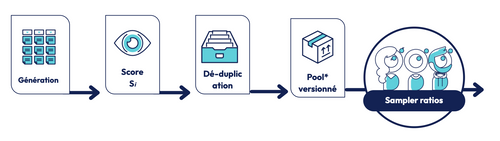
3.5. Génération pilotée par prompts : « c'est bon » veut dire quoi ?

Avant d'intégrer une image synthétique, elle traverse trois contrôles successifs.

La première porte vérifie la plausibilité physique. On mesure que la modification reste confinée à la soudure ( IoU > 0.8 ) et que la texture métallique est préservée (cohérence des histogrammes d'intensité). L’absence de ruptures de gradient garantit une transition naturelle entre réel et synthétique.

La deuxième porte évalue l'utilité pour l'apprentissage. En projetant les images dans un espace d'embeddings, on vérifie qu'elles ne sont ni trop redondantes (proches d'échantillons existants) ni trop exotiques (hors domaine industriel). Des stratégies comme k-center ou DPP maximisent la diversité du dataset.

La troisième porte détecte les artefacts de génération. On entraîne un classifieur "réel vs synthétique" : s'il est trop performant, le modèle principal risque d'exploiter des motifs artificiels plutôt que les vrais défauts. On teste aussi par ablation : si retirer la zone générée ne change pas le score KO, l'image est rejetée (le défaut n'apporte pas d'information discriminante).

Ces trois filtres garantissent que chaque image mérite sa place dans le POOL★.

3.6. La métrique du plausible, mesurer la distance entre vrai et simulé

Dire qu’une image synthétique est plausible signifie qu’elle est mesurable. Les métriques classiques comme SSIM ou FID ne mesurent que la similarité d’images de manière générique, sans tenir compte du contexte du use case.

À la place, une distance composite entre une image réelle x et une image synthétique x’ a été définie.

Dplaus*(x, x’) = αDCLIP(x, x’) + βDphys(x, x’)*

La première partie DCLIP​ mesure la cohérence visuelle globale dans un espace sémantique (avec un encodeur CLIP). Mais CLIP peut être trompé quand 2 images ont 2 fonds différents mais des défauts identiques. D’où la seconde composante.
La seconde, Dphys​ évalue la conformité physique, à savoir la distribution des intensités lumineuses (reflets), la régularité des gradients au bord du cordon et la continuité géométrique du défaut.

Une petite distance Dplaus signifie que l’image générée respecte les contraintes physiques du monde réel, même si elle n’existe pas.
Évidemment ce n’est pas une garantie absolue car certaines images peuvent contourner la métrique, mais cela permet de rendre objectivable la notion de plausible. Au lieu de juger à l’œil, on mesure (ouverture sur l’ingénierie du faux, construire des critères quantifiables pour valider ce qui n’a pas été observé).

4. Le procès en légitimité du faux

L’expérimentation repose sur trois configurations, d’abord un modèle entraîné uniquement sur des données réelles (baseline), un autre combinant réel et données synthétiques filtrées et enfin une version intégrant des données synthétiques non filtrées.

Chaque approche est évaluée selon plusieurs critères dont la performance (F1 sur la classe KO, rappel, précision), la calibration de la confiance (ECE, Expected Calibration Error, Naeini 2015), la robustesse aux perturbations (rotation, flou, bruit) et la détection des contextes hors distribution (OOD).
Aussi, l’évaluation intègre la dimension économique via l’espérance de coût

E[C] = cFN*FN + cFP*FP

où cFN ≫ cFP en inspection industrielle, cFN et cFP étant les coûts unitaires, FN et FP étant respectivement les faux négatifs et faux positifs. (Dans notre cas, la classe positive est la classe KO, on considère donc qu’un “positif” = une soudure défectueuse).

Pourquoi optimiser le coût plutôt que l'accuracy ?

Toutes les erreurs ne coûtent pas pareil. Dans l’inspection de soudures, un faux négatif, une soudure défectueuse jugée bonne peut coûter des milliers d’euros (responsabilité légale, image de marque). À l’inverse, un faux positif, une soudure saine écartée à tort, ne coûte qu'une inspection manuelle, soit quelques dizaines d’euros. Autrement dit, cFN ≫ cFP (jusqu’à 100 à 1000 fois plus).

L’espérance de coût représente donc le coût moyen par décision, pondéré par la gravité économique de chaque type d’erreur.

Pourquoi ne pas optimiser l'accuracy ?

Optimiser l’accuracy n’a pas tellement de sens ici car elle considère FN et FP comme équivalents. Sur un dataset déséquilibré, un modèle qui dirait toujours OK aurait 98 % d’accuracy mais serait désastreux en pratique. En optimisant E[C], on intègre cette asymétrie en acceptant un peu plus de faux positifs si cela permet de réduire drastiquement les pertes réelles.

4.1. Analyse de sensibilité et causalité : qu’est-ce qui compte vraiment ?

Prouver que le pipeline fonctionne, c’est bien. Mais comprendre pourquoi il fonctionne, c’est mieux. L’étude a porté sur la sensibilité des performances du modèle aux paramètres du pipeline, avec à la fois le degré d’édition (“strength”), l’influence du prompt textuel (“guidance”), le nombre d’étapes de diffusion, le seuil de filtrage S*_i* ou encore le ratio entre réel et synthétique.

À l'aide d'une analyse de Sobol (Sobol, 1993, méthode de décomposition de variance pour l'analyse de sensibilité globale), la part de F1_score est mesurée par chaque paramètre. Le résultat montre que l’intensité d’édition et le ratio de mix dominent. Si on édite trop légèrement, les défauts ajoutés sont insignifiants. Trop fortement, on casse la texture réelle.

Une valeur marginale par image (inspirée des Shapley values => issu de la théorie des jeux coopératifs (Shapley, 1952) et récemment adapté au machine learning) est calculée pour estimer quelles images contribuent vraiment au gain. La surprise : moins de 10 % des images expliquent la majorité du progrès. Certaines images sont neutres voire nuisibles. D'où l'importance d'une gouvernance stricte.

Enfin, l’effet de modifier uniquement la géométrie du défaut ou sa texture est testé, la géométrie influence surtout le rappel (le modèle trouve plus de défauts), la texture joue davantage sur la calibration (le modèle estime mieux sa confiance). Dans un contexte industriel, mieux vaut un modèle qui détecte davantage, quitte à douter, qu'un modèle trop confiant mais aveugle.

5. Quand le faux améliore le vrai

C’est le paradoxe du projet, des images qui n’existent pas rendent les modèles plus fiables sur celles qui existent.

L’ajout contrôlé de 15 % d’images synthétiques (ratio KO ≈ 28,3 %) augmente :

• le rappel KO (moins de défauts ratés),
• la calibration (le modèle sait quand il doute),
• la robustesse hors distribution.

Le modèle élargit ses frontières de décision dans les zones où P(X|Y = KO) était vide. Une courbe coût bénéfice montre que le point d’équilibre entre coût GPU / gain métier se situe autour de 7 000 images.

6. Vers une écologie du synthétique

La donnée synthétique pose une question éthique et énergétique, combien de “faux” faut-il pour produire un “vrai” progrès ?

6.1. Écologie computationnelle

Chaque génération consomme de l’énergie. Sur un GPU T4 utilisé sur Kaggle (environ 70 W en charge), une image Stable Diffusion nécessite environ 5 secondes de calcul. L’énergie consommée par image se calcule simplement par :

E*_i*mage = P*t = 70W * 5 / 3600 h ≈ 0,1 Wh

Pour une campagne de 12 000 images, cela représente donc environ :

E_total = 12 000*0,1 Wh ≈1,2 kWh

Optimiser la génération revient donc aussi à une forme de sobriété algorithmique : réduire les steps, utiliser le FP16, grouper les batches GPU ou éliminer les prompts redondants permet de diminuer significativement cette empreinte.

6.2. Écologie cognitive

Un système bouclé (générer — entraîner — régénérer) dérive rapidement et on connaît souvent une amplification des biais du modèle. Il faut maintenir une injection de réel nouveau. Le risque de la boucle fermée est que si on génère à partir d'un modèle, qu'on entraîne un nouveau modèle sur ce généré, puis qu'on régénère avec ce nouveau modèle, on amplifie les biais et on perd progressivement la diversité (collapse, phénomène documenté dans la doc récente sur les modèles génératifs (Shumailov, 2023).

Par exemple, si le modèle a une légère préférence pour les fissures verticales, génération 1 produit 60% de verticales. On entraîne dessus, génération 2 produit 75% de verticales, génération 3 => 90%, etc. Finalement, on a oublié que des fissures obliques existent, il faut toujours maintenir une proportion significative de données réelles neuves.

6.3. Écologie épistémique

Chaque image synthétique doit être traçable, documentée, falsifiable. Le POOL★ devient ainsi une archive de ce qui est possible et versionnée, vérifiable. L’avenir de l’IA industrielle sera hybride et traçable. Créer du faux, c’est prendre position sur ce qu’on considère comme “vrai”.
C’est accepter que l’IA industrielle ne se nourrit pas uniquement du réel, mais aussi de sa projection contrôlée.

En générant des images impossibles, on apprend parfois à voir ce que le réel, trop rare, nous cache.

7. Explorer les prolongements, une génération et une interprétation plus conscientes ?

Pour résumer, le pipeline construit repose sur un principe clair, on part du réel, on essaye de le comprendre et sur cette base on l’étend.
Chaque image synthétique provient d’une image de soudure réelle, segmentée, masquée et éditée via diffusion. Mais cette méthode n’épuise pas le champ des possibles…

7.1. Prolonger le réel plutôt que le recréer

Le processus mis en place reste local car il agit sur un patch et non sur la représentation globale de la soudure. Une perspective consiste à projeter l’image entière dans l’espace latent du modèle de diffusion (latent inversion) en encodant l’image KO réelle x*_0* dans l’espace latent z₀ = EΦ(x₀ ) , puis on la fait légèrement évoluer selon une direction de défaut Δz : z’ = z₀ + η*Δz , où Δz est une variation sémantique identifiable (profondeur de fissure, changement de texture, intensité d’oxydation).

Le décodeur de diffusion D_θ​ reconstruit ensuite une image x’ = D_θ(z’) , une sorte de clone basée sur l’image réelle mais située un peu plus loin dans l’espace des défauts. Ce glissement contrôlé permet d'explorer des nuances invisibles dans le dataset d’origine et de générer des séries de défauts cohérents, paramétrés. Cette technique est issue des modèles de Blended Latent Diffusion (Avrahami, 2023. Blended Latent Diffusion) et conserve les propriétés physiques de l'image initiale tout en offrant un contrôle sémantique beaucoup plus fin.

7.2. Un modèle qui sait qu’il ne sait pas

Mais plus on crée de diversité, plus on expose le modèle à l’inattendu. Un bon modèle n'est pas celui qui “devine” toujours, mais celui qui sait quand il doute. Il doit être capable d'estimer l'incertitude de ses prédictions et de refuser de conclure quand l'image sort de son domaine de compétence.

Une méthode consiste à calculer l'entropie de la sortie d'un classifieur f_ፀ(x) :

u(x) = -∑_k ( p_θ(y_k|x)logp_θ(y_k|x) )

Cette formule de Shannon mesure la dispersion de la distribution de probabilités prédite. Pour notre problème binaire (OK/KO), si p(KO)=0.99 => u = 0.08 bit (quasi-certitude), si p(KO)=0.50 => *u = 1 * bit (incertitude maximale). Plus l'entropie u(x) est élevée, plus le modèle hésite. On définit alors un seuil au-delà duquel le modèle passe en zone d'incertitude, là où se logent souvent les images synthétiques mal calibrées ou les nouveautés du terrain.

Dans un pipeline industriel, cette conscience du doute est un mécanisme de sûreté. Si un modèle devient trop confiant sur tout, c'est un signal d’alerte. Un modèle bien calibré maintient une marge d'humilité. Ces deux prolongements convergent vers l’idée d’une IA industrielle qui ne se contente pas de produire mais qui rend compte de la façon dont elle le fait.

Conclusion

Cet article a exploré un territoire paradoxal : celui où des images qui n'ont jamais existé permettent de mieux voir ce qui existe réellement. En partant de la détection de défauts de soudure, nous avons montré que la donnée synthétique n'est ni une imposture ni un artifice, mais un outil épistémique répondant à une contrainte industrielle fondamentale : comment apprendre de ce qu'on ne voit presque jamais ?

La réponse ne réside pas dans l'accumulation aveugle de faux, mais dans leur fabrication contrôlée et traçable. Le pipeline présenté démontre qu'il est possible d'enrichir la distribution d'apprentissage sans trahir la physique du réel. Les résultats le confirment : 15% de données synthétiques bien choisies suffisent à améliorer significativement le rappel, la calibration et la robustesse du modèle.

Au-delà de la performance, c'est une posture qui se dessine. Celle d'une IA industrielle qui compose avec le vrai et le faux pour mieux servir la décision humaine. Une IA qui sait douter, qui trace ses sources, qui mesure l'utilité de chaque image. Une IA qui, paradoxalement, devient plus fiable en acceptant d'apprendre aussi du simulé.

L'avenir de cette approche dépasse la soudure. Partout où les anomalies sont rares ou dangereuses à observer – imagerie médicale, surveillance d'infrastructures – la génération synthétique ouvre des espaces d'apprentissage inaccessibles autrement. À condition de maintenir une écologie du synthétique : sobre, vigilante, rigoureuse.

Car fabriquer du faux pour améliorer le vrai, c'est accepter de définir ce qui mérite d'être généré, tracé, intégré. C'est reconnaître que l'IA industrielle ne se contente plus de refléter le monde : elle contribue à en explorer les possibles et à en révéler les angles morts.

Et si, finalement, le synthétique nous apprenait à mieux regarder le réel ?

Remerciements

Nous tenons à remercier chaleureusement TOUL, MAFA, PHIL, BAPO et CYRB pour leurs relectures attentives et la qualité de leurs feedbacks, qui ont grandement contribué à l’amélioration de cet article.

Références

Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal.
Kirillov, A.,... (2023). Segment Anything. arXiv preprint arXiv:2304.02643.
Rombach, R., Blattmann, A., Lorenz, D., Esser, P., Ommer, B. (2022). High-Resolution Image Synthesis with Latent Diffusion Models. CVPR.
Radford, A.,... (2021). Learning Transferable Visual Models From Natural Language Supervision (CLIP). ICML.
Goodfellow, I.,... (2014). Generative Adversarial Networks. NeurIPS.
Wang, Z.,... (2004). Image Quality Assessment: From Error Visibility to Structural Similarity (SSIM). IEEE TIP.
Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., Hochreiter, S. (2017). GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium (FID). NeurIPS.
Naeini, M. P., Cooper, G., Hauskrecht, M. (2015). Obtaining Well-Calibrated Probabilities Using Bayesian Binning into Quantiles (ECE). AAAI.
Hendrycks, D., Gimpel, K. (2016). A Baseline for Detecting Misclassified and Out-of-Distribution Examples in Neural Networks. ICLR Workshop.
Sobol, I. M. (1993). Sensitivity Estimates for Nonlinear Mathematical Models. Mathematical Modelling & Computational Experiments.
Shapley, L. S. (1952). A Value for n-Person Games. Contributions to the Theory of Games.
Kulesza, A., Taskar, B. (2012). Determinantal Point Processes for Machine Learning (DPP). Foundations and Trends in ML.
Avrahami, O., Fried, O., Lischinski, D. (2023). Blended Latent Diffusion.
Shumailov, I., et al. (2024). The Curse of Recursion: Training on Generated Data Makes Models Forget.