NLP : une classification multilabels simple, efficace et interprétable
Le Machine Learning nous permet aujourd’hui de classifier facilement du texte ; or, le texte appartient parfois à plusieurs catégories, d’où le nom de classification multilabels pour parler de cette tâche. Nous allons voir dans cet article comment traiter ce problème, évaluer la performance de nos algorithmes et les interpréter.
Avant toute chose, le code est disponible sur Github. Il contient deux web-apps : une permettant d’entraîner un modèle sur son propre dataset et une permettant d’afficher les prédictions et de les interpréter. A noter que ce modèle correspond à un ensemble de sous-modèles.
La web-app permettant d’afficher les prédictions est également accessible directement depuis un navigateur. Il faut écrire des phrases en anglais car comme expliqué plus loin dans l’article, le modèle a été entraîné sur un corpus anglais.
1 - Le NLP et la classification multilabels
Tout au long de notre article, nous avons choisi d’illustrer notre article avec le jeu de données du challenge Kaggle Toxic Comment. Ce jeu est constitué de commentaires provenant des pages de discussion de Wikipédia. Le but du challenge est d’être capable de détecter différents types de toxicité tels que les menaces, les insultes, l’obscénité, et la haine raciale à partir de ces commentaires. Un commentaire peut alors appartenir à plusieurs de ces classes. D’avance donc, nous nous excusons pour les insultes et termes choquants que vous pourrez rencontrer.
Nous allons dans un premier temps expliquer ce qu’est la classification multilabels. Elle consiste simplement à dire qu’au lieu d’attribuer une seule classe à une instance donnée, cette instance peut appartenir à plusieurs classes. La classification multilabels a des usages courants dans la vie de tous les jours : par exemple, un film appartient souvent à plusieurs genres à la fois.
Or, les algorithmes de classification existants ont été construits pour attribuer une seule classe à une instance, il est donc nécessaire de transformer notre problème multilabels en de multiples problèmes binaires unilabel (c’est une sorte de one-hot encoding). comme l’illustre le schéma qui suit :

Une fois notre problème multilabel transformé en des problèmes binaires unilabel, il nous reste à construire pour chaque classe un classifieur binaire unilabel. Ces classifieurs sont entraînés indépendamment sur l’ensemble des données d'entraînement. Dans notre exemple précédent, nous aurons ainsi un modèle pour déterminer l’appartenance d’un film au genre Fantastique, un modèle pour le genre Aventure, un modèle pour le genre Drame et un modèle pour le genre Romance. Cette méthode est connue pour sa simplicité et sa complexité linéaire. En revanche, un inconvénient est qu’elle ne prend pas en compte les possibles corrélations entre les différentes classes, puisqu’elle traite chaque classe indépendamment. D’autres méthodes comme les chaînes de classifieurs existent.
2 - Un modèle simple, efficace et interprétable à base de Bag of Words et de Régressions Logistiques
Dans un premier temps, nous avons transformé nos commentaires sous forme de liste de tokens. Il s’agit d’une étape essentielle du traitement de texte qui consiste à découper une phrase en une liste des mots la constituant. Seulement, les modèles de machine learning peuvent être entraînés uniquement sur des entrées de valeurs fixes bien définies et surtout numériques, ce qui n’est pas le cas des tokens, puisque chaque commentaire à une longueur différente et qu’il s’agit de mots. Il est nécessaire de représenter numériquement nos données contextuelles. Pour cela, il existe une méthode simple et largement connue appelée Bag of Words (BoW).
Les BoW sont des méthodes utilisées pour extraire les features d’un texte. Un BoW est une représentation de texte qui décrit l'occurrence de mots dans un texte, en mesurant la présence de mots connus dans un corpus. Elle s’appelle ‘bag’ of words puisqu’elle ne prend pas en compte l’ordre ni la structure des mots dans le document.

Pour cela, nous avons d’abord rempli les textes vides de notre texte par un mot “unknown”, c’est ce que fait notre méthode preprocess_train_df() dans le snippet de code ci-après. Ensuite, nous avons utilisé le CountVectorizer de scikit-learn, qui consiste exactement à créer des vecteurs comme ceux de l’image ci-dessus. Nous aurions pu utiliser TfidfVectorizer, qui donne plus de poids aux mots rares, mais le CountVectorizer a pour avantage d’indiquer le nombre d’occurrences d’un mot dans une phrase, ce qui permet de faciliter l’intuition derrière l’interprétation de nos prédictions. Nous reviendrons sur cet aspect dans la partie interprétabilité.
train_df = preprocess_train_df(train_df, COMMENT_COLUMN)
vectorizer = CountVectorizer(ngram_range=(1, 1), tokenizer=tokenize, min_df=3, max_df=0.9, strip_accents='unicode')
X = vectorizer.fit_transform(train_df[COMMENT_COLUMN])
y = train_df[LABELS]
Une autre propriété très importante de la régression logistique est que ses prédictions correspondent vraiment à des probabilités au sens statistique, puisqu’il s’agit exactement de la loi logistique standard de paramètre (0,1) ; cela peut paraître évident mais c’est pourtant très rare qu'un modèle soit bien calibré. Or, savoir qu’une phrase a 99% de chances d’être dans une catégorie plutôt que 51% peut avoir un gros impact sur la décision finale !
Aparté sur le compromis performance - interprétabilité
Notons qu’il y a un compromis à choisir entre un modèle performant, complexe à interpréter, et un modèle un peu moins performant, simple à interpréter. Le curseur de notre côté a été placé du côté de la simplicité, parce que le combo BoW / régression logistique est une approche déjà efficace et va nous permettre d’interpréter les choix du modèle à l’échelle du mot.
Pour placer le curseur côté performance, l’état de l’art en classification de texte se fait avec des BERT, seulement ces modèles ne sont pas interprétables par nature bien qu’il existe des méthodes telles papier de Stanford, surprenante en terme de performance malgré sa simplicité, consiste à partir du théorème de Bayes, de calculer un rapport de ratios. En particulier, un ratio est calculé pour chaque mot et correspond à sa fréquence dans les documents d’une classe donnée. On obtient donc le rapport de ratio d’appartenance du mot à la classe 1 sur le ratio d’appartenance du mot à la classe 0. Ces features sont donnés à un SVM ou une régression logistique. Sur cette dernière méthode, l’ajout de bigrammes apporte un gain significatif ; quant à son interprétabilité, on peut toujours interpréter les poids de la régression logistique mais qui seront liés à des features plus difficiles à interpréter qu’une simple présence ou absence d’un mot.
Pour entraîner nos régressions logistiques, nous avons bouclé sur les différentes colonnes en target, en utilisant à chaque fois les mêmes features, notre BoW, comme le décrit le code ci-après :
LOGISTIC_REGRESSION_PARAMETERS = {‘C’: 0.1,
‘max_iter’: 100}
def fit_one_classifier(X, y):
y = y.values
classifier = LogisticRegression(**LOGISTIC_REGRESSION_PARAMETERS)
return classifier.fit(X, y)
def fit_all_classifiers(X, y_full, labels):
classifiers = {}
for idx, label in enumerate(labels):
target = y_full[label]
classifier = fit_one_classifier(X, target)
classifiers[label] = classifier
return classifiers
Nos régressions logistiques entraînées sont désormais stockées comme valeurs dans un dictionnaire, avec leur classe en clés.
3 - Evaluation de notre ensemble de modèles
Les métriques utilisées pour évaluer nos modèles diffèrent légèrement d’une simple classification unilabel. Dans une classification unilabel, l’Accuracy est une des métriques largement utilisées :

Avec VP les vrais positifs, VN les vrais négatifs, FP les faux positifs et FN les faux négatifs.
Concernant notre problème de classification multilabels, la prédiction de deux labels sur trois devrait avoir un meilleur score que la prédiction d’aucun label. Une des méthodes employées est d’évaluer la prédiction pour chaque label indépendamment et de prendre la moyenne de ces évaluations. Il est cependant déconseillé d'utiliser l’accuracy sur des problèmes déséquilibrés, car pour avoir une accuracy élevée il suffirait de simplement bien classifier les observations de la classe majoritaire. Or, notre jeu de données est bien déséquilibré, donc l’accuracy n’est pas la meilleure métrique à utiliser pour notre exemple.
Nous avons donc utilisé la ROC AUC moyennée par colonne. En d’autres termes, le score est la moyenne des AUCs individuelles pour chaque colonne prédite (chaque label). Pour rappel, la ROC AUC (Area Under the ROC Curve) est une métrique géométrique définie par l’aire sous la courbe paramétrique du rappel (taux de vrais positifs) en fonction du taux de faux positifs obtenue pour différents seuils de classification. Diminuer la valeur du seuil de classification permet de classer plus d’élément comme positifs, ce qui augmente le nombre de faux positifs et de vrais positifs.
Seulement, elle s’avère être aussi moins efficace dès lors que l’on travaille avec des classes déséquilibrées, car elle prend en compte les vrais négatifs et ces derniers ont un effet non négligeable sur la tenue de la métrique en fonction du niveau de déséquilibre du dataset. Par souci de simplicité nous somme restés sur cette métrique.
Une alternative aurait été d’utiliser la PR AUC (Precision-Recall) qui est l’aire en dessous la courbe paramétrique de la précision par rapport au rappel, car les métriques de precision-recall ne s’occupent pas des vrais négatifs.
Précision :
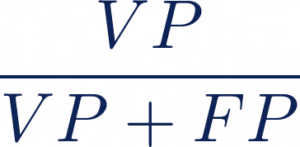
Rappel :
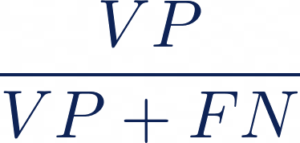
Il existe également d’autres métriques utilisées comme la Hamming-Loss (HL). Cette métrique correspond à la proportion de labels mal prédits, c’est à dire la fraction de labels faux sur le nombre total de labels :
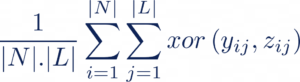
Si nous considérons le cas binaire, on obtient donc : HL = 1- Accuracy. Cette métrique peut donc aussi être une solution au problème de classes déséquilibrées.
Dans notre cas, notre ROC AUC moyenne est de 0.95. A noter que cette métrique atteint autour de 0.98 avec des features et modèles plus complexes (donc peu interprétables). Le code suivant permet de la calculer sur nos différents modèles en validation croisée :
def cross_val_score_classifier(X, y):
classifier = LogisticRegression(**LOGISTIC_REGRESSION_PARAMETERS)
cv_score = mean(cross_val_score(classifier, X, y, cv=3, scoring=‘roc_auc’))
return cv_score
def compute_CV_score_for_each_class(X, y_full, labels):
scores = []
for label in labels:
target = y_full[label].values
cv_score = cross_val_score_classifier(X, target)
scores.append(cv_score)
return scores
La régression logistique est intéressante parce qu’elle est intrinsèquement interprétable. Elle est de plus monotone, ce qui facilite sa compréhension : lorsque l’on ajoute une variable à poids positif, la prédiction augmente, et inversement pour un poids négatif.
Voyons comment interpréter notre modèle, de façon globale (à l’échelle du corpus de texte, quels mots ont un impact “positif” ou “négatif” sur la prédiction) et de façon locale (à l’échelle d’une phrase**)**.
Rappelons pour cela la formule de la régression logistique. La régression linéaire, définie par la formule qui suit, ne convient plus pour nos outputs de 0 ou 1 :
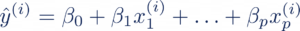
avec yhat la prédiction de l’observation i, x~j ~ les features, ß~j ~ les poids.
Nous la passons donc à travers une fonction sigmoïde définie comme telle, pour écraser les valeurs entre 0 et 1 :
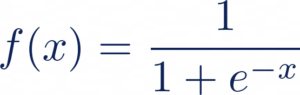
Ce qui nous donne la probabilité d’appartenance à la classe 1 suivante :
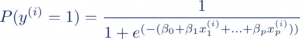
Maintenant, si nous voulons interpréter l’importance d’une feature xj en particulier, il faut que nous isolions son poids associé ßj . Pour cela, il est nécessaire de passer par l’expression des “odds” obtenue en résolvant l’équation ci-dessus. Les odds correspondent au ratio de la probabilité d’appartenance à la classe 1 sur la probabilité d’appartenance à la classe 0 :

Partant de l’équation ci-dessus, nous utilisons la propriété de l’exponentielle pour isoler le poids associé à la feature qui nous intéresse, ici ß~j ~ . Pour cela, nous augmentons la valeur de notre feature xj de 1 ce qui nous donne le oddsxj+1 et nous calculons le rapport de odds_xj+1_ avec odds (notre ratio d’origine):
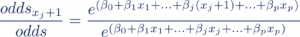
Ce qui nous donne, après simplification :
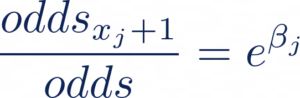
Et de même, si nous diminuons la valeur de notre feature xj de 1, nous obtenons:
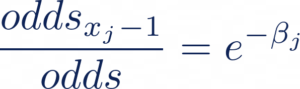
C’est là que la propriété de notre CountVectorizer est intéressante. En comptant simplement le nombre d’occurrences de mots dans une phrase, il est plus facile d’incrémenter une feature de 1. Si nous ajoutons le mot j initialement absent dans la phrase, alors son compte passe de 0 à 1, ce qui multiplie les odds par l’exponentielle de son poids ßj. Au contraire, si nous supprimons un mot j de la phrase, les odds sont multipliés par l’exponentielle de la négation de son poids.
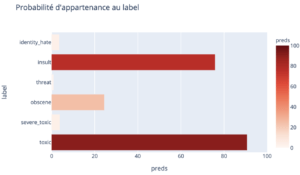
Prenons un exemple. Si nous prenons la phrase “You are a real idiot”, notre modèle nous donne une probabilité de 76% d’appartenance à la catégorie insulte.
Regardons les poids de la régression logistique associés à chaque mot, toujours pour cette catégorie insulte :
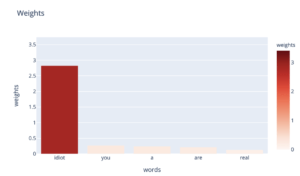
Nous voyons que le mot “idiot” a un poids prépondérant, ici de 2.8, sur notre prédiction. Maintenant, comment la présence de ce mot influe réellement sur la valeur de notre prédiction ?
Pour comprendre, calculons nos odds. Ici, nos odds valent 0,76/(1-0.76) = 3,17 fois plus de chances d’appartenir à la catégorie insulte que de ne pas en faire partie.
Si l’on se réfère à la formule de l’évaluation des odds, si nous retirons ce mot, les oddswith_idiot sont multipliés par l’exponentielle de la négation de son poids, autrement dit :
oddswithout_idiot= oddswith_idiot * exp(-poidsidiot) = 3.17 * exp(-2.8) = 0.19.
Ce qui veut dire qu’en enlevant “idiot” , il n’y a que 0.19 fois plus de chances d’appartenir à la catégorie insulte que de ne pas en faire partie ! Ce qui en terme de probabilités, correspond à une prédiction de 16% sur la classe insulte.
Si nous repartons de notre phrase d’origine “You are a real idiot”, et que nous la modifions légèrement pour la rendre plus insultante : “Y_ou are a real fat idiot”_ , voyons comment le mot “fat” modifie nos prédictions.
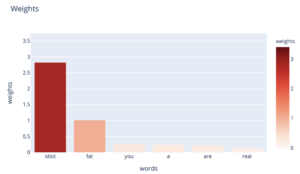
La régression logistique associe un poids de 1 à notre mot “fat”. Nous avions 3,17 fois plus de chances d’appartenir à la catégorie insulte avant l’ajout de ce mot ; en ajoutant ce mot, nous multiplions ces odds par exp(1), et nous avons de ce fait 8.61 fois plus de chances d’appartenir à la catégorie insulte. En terme de probabilités, nous passons donc de 76% à 89,6%.
Voici la méthode nous permettant de récupérer les poids des mots de notre phrase. Nous récupérons d’abord uniquement les mots de notre BoW qui sont présents dans notre phrase : ici, test_term_doc correspond à notre phrase vectorisée, et le BoW étant une gigantesque matrice creuse, le .indices nous permet de récupérer les valeurs non nulles dans notre BoW.
De la même façon, les poids associés à ces mots sont récupérés pour la régression logistique de la catégorie voulue. Enfin, le résultat est retourné dans un DataFrame dont les valeurs sont ordonnées par poids, du plus grand au plus petit.
def get_local_weights_df(vectorizer, test_term_doc, classifiers, label):
words = np.array(vectorizer.get_feature_names())[test_term_doc.indices]
weights = classifiers[label].coef_.ravel()[test_term_doc.indices]
df_words_weights = pd.DataFrame({‘words’: words, ‘weights’: weights}).sort_values(ascending=False, by=‘weights’)
return df_words_weights
Nous pouvons aussi voir les poids globaux associés à une catégorie. Cette fois, la méthode est plus simple, il suffit simplement de récupérer les coefficients et les mots de notre BoW sans avoir à filtrer.
def get_global_weights_df(vectorizer, classifiers, label):
feature_importance = classifiers[label].coef_[0]
words = vectorizer.get_feature_names()
df_words_weights = pd.DataFrame({‘words’: words, ‘weights’: feature_importance})
df_words_weights = df_words_weights.sort_values(ascending=False, by=‘weights’)
return df_words_weights
Ce qui nous donne le graphe suivant pour la catégorie insulte :
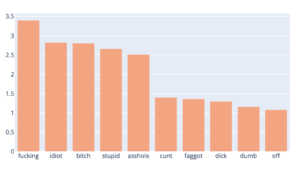
Nous voyons que de beaux noms d’oiseaux ont été détectés comme impactants par notre classifieur pour la catégorie insulte.
Conclusion
Finalement, nous avons effectué notre tâche de classification multilabels en la transformant en de multiples classifications binaires. Nous avons alors opté, au risque de paraître psittacin, pour des modèles simples, efficaces et interprétables. Par opposition à d’autres modèles plus performants mais bien plus complexes -et c’est là que le bât blesse- comme les réseaux de neurones profonds, nous sommes convaincus que la simplicité de certains modèles pourra aider à une adoption à plus grande échelle du Machine Learning.