Classer ses dépenses à l’aide de la classification bayésienne naïve

le 30/11/2011 par Antoine Gaudelas

Les problèmes de classification constituent une famille de problèmes auxquels il est possible d’appliquer des méthodes d’apprentissage supervisé, c’est-à-dire où l’on dispose d’une base d’exemples correctement identifiés. Le but consiste, à partir de ces exemples, de construire un modèle capable de prédire avec un bon degré de confiance à quelle classe (chat, oie, canard, papillon…) appartient un individu à partir de la seule connaissance de certaines de ses caractéristiques (ailes, pattes, bec, moustaches, cri…). Nous allons étudier ici sur la base d’un exemple concret un type de modèle de classification en particulier : le classifieur Bayésien naïf.

Sa caractéristique principale est qu’il émet une hypothèse forte a priori inadaptée aux cas pratiques : l’indépendance des caractéristiques étudiées. En termes simples, un classifieur bayésien naïf suppose que l'existence d'une caractéristique déterminant l’appartenance à une classe est indépendante de l'existence d'autres caractéristiques. Par exemple, un animal sera considéré avec un bon degré de confiance comme un canard s’il a des ailes, un bec et qu’il cancane comme un canard, en ignorant totalement la possibilité que ces caractéristiques puissent être corrélées.

En dépit d’une conception simpliste, ces modèles font preuve dans beaucoup de situations réelles d’un pouvoir de prédiction étonnamment supérieur à d’autres modèles concurrents, comme par exemple les arbres de décision. Une part du voile sur les raisons sous-jacentes à ce paradoxe apparent a été levée en 2004 (consulter la référence à ce sujet en fin d’article pour plus de détails). En termes simples, le modèle naïf se comporte d’autant mieux que le nombre de classes parmi lesquelles choisir est faible. Ceci est dû en bonne partie au fait que le degré de certitude avec laquelle ils prennent leur décision peut se permettre d’être médiocre tout en restant suffisant, par un effet de seuil. D’autre part, plus la répartition de la covariance des caractéristiques est distribuée équitablement entre les différentes classes, plus leurs contributions respectives à une mauvaise classification auront tendance à s’annuler dans l’estimation finale de la probabilité d’appartenance à une classe donnée : en d’autres termes, il sont relativement peu sensibles au bruit dès lors que la contribution de quelques caractéristiques à une classe « pèse » suffisamment lourd.

On trouve aujourd’hui des algorithmes qui ont de meilleurs résultats empiriques tels que les plus proches voisins ou les séparateurs à vaste marge (qui seront traités dans un article ultérieur). Toutefois, les classifieurs bayésiens naïfs conservent l’avantage avec des échantillons de taille réduite sur lesquels ils convergent plus rapidement pour estimer les paramètres nécessaires à la classification.

D’autre part, l’hypothèse d’indépendance épargne le calcul de la covariance et permet de travailler avec une base d’exemples croissant linéairement avec le nombre de caractéristiques, ce qui confère un avantage immédiat en termes de calculabilité.

Le modèle bayésien naïf

Le modèle probabiliste pour un tel classifieur est le modèle conditionnel P(X | x₁,…,x_n), où X est la variable « de classe » (celle qui indique si un individu appartient à une classe donnée) conditionnée par plusieurs variables caractéristiques x_i (par exemple l’obésité, le diabète, le cholestérol dans le cas d’une classification binaire « risque cardiovasculaire ou non »). Le théorème de Bayes s’énonce avec nos notations de la manière suivante :

"eq02"

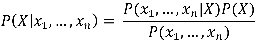
Ici, le dénominateur correspond à la répartition des caractéristiques au sein de la population des individus, il est donc indépendant de la variable de classe X elle-même.

Le numérateur quant à lui peut s’écrire, par application de la formule de Bayes (c’est-à-dire la définition de la probabilité conditionnelle, soit P(X,Y) = P(X|Y)P(Y)) :

"eq03"

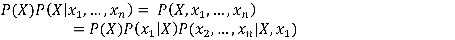
On poursuit alors en développant le dernier membre :

"eq04"

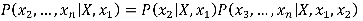
On itère ensuite de la sorte jusqu’à avoir développé les n caractéristiques. C'est ici qu’intervient l'hypothèse d’indépendance des caractéristiques (ou hypothèse naïve) : si les x_i sont indépendants deux à deux, alors P(x_i|X,x_j) = P(x_i|X). Ce qui fait que les facteurs conditionnés par X, d’une part, et des x_i d’autre part, peuvent être récrits sous la forme de probabilités conditionnées par X seulement, de sorte que l’expression se réduit en fin de compte à la forme suivante :

"eq07"

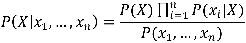
Soit en français :

Membre de gauche : la probabilité qu’un individu appartienne à une classe donnée sachant qu’il possède les caractéristiques x₁,…,x_n est égal à
Membre de droite : la probabilité de distribution de la classe dans la population, pondérée par l’occurrence de chaque caractéristique pour cette classe et une constante (le dénominateur).

A titre de remarque, ce dénominateur est appelé évidence (du faux-ami anglais evidence), que l’on peut estimer à partir d’un ensemble d’entraînement constitué d’un échantillon d’individus aux classes connues et supposé représentatif. En pratique cependant, il ne dépend que des caractéristiques pour lesquels on cherche à déterminer la loi de probabilité d’appartenance à une classe : dans le calcul du maximum de l’expression, il agit donc comme une constante comprise entre 0 et 1 que l’on peut donc tout simplement choisir d’omettre de calculer.

Si X peut prendre les valeurs c₁,…,c_k (k classes distinctes), alors le modèle ainsi obtenu dépend des paramètres suivants :

- P(x_i | X = c_j)- P(X=c_i)

Ce sont ces paramètres que l’on va chercher à estimer dans le cadre d’un apprentissage.

Estimation des paramètres du modèle

Les paramètres (distribution des classes et des caractéristiques) peuvent être estimés par les fréquences des classes par rapport aux caractéristiques sur la base d’exemples d’individus dont les classes sont connues (notre ensemble d’entraînement). Il est nécessaire de choisir a priori une distribution pour les classes et pour les caractéristiques. Elles dépendront en pratique du type de valeurs rencontrées (par exemple pour des caractéristiques binaires, on choisira une loi de Bernoulli, à valeurs discrètes une loi multinomiale, à valeurs continues une loi normale). L’approximation fréquentielle reviendra à calculer les valeurs suivantes :

"eq10"

"eq11"

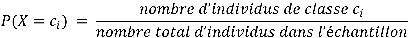
En pratique, si l’on n’a pas la garantie que notre échantillon contienne des représentants de chacune des classes, on affectera une probabilité arbitraire à ces classes « manquantes » (on choisira alors souvent une distribution équiprobable pour les classes manquantes : P(X=c) = 1/k). La même tactique s’applique si des caractéristiques ne sont pas représentées. Plusieurs stratégies, dite de lissage, sont alors possibles (la plus connue étant le lissage de Laplace, qui consiste à ajouter artificiellement une occurrence de chaque mot aux exemples d’entraînement). Ces techniques permettent d’éviter que des caractéristiques sur lesquels nous ne disposons pas d’information dans la phase d’entraînement n’annulent purement et simplement la probabilité d’appartenance à une classe dans notre modèle lors de l’étape de prédiction.

Construction d’un classifieur à partir d’un échantillon

Nous savons désormais calculer les paramètres de notre modèle. Il manque pour fabriquer un classifieur à proprement parler une règle de décision qui puisse les exploiter. La règle la plus simple consiste à évaluer la probabilité de chaque classe c compte tenu des caractéristiques de l’individu et de choisir celle qui maximise l’expression du numérateur, soit

"eq13"

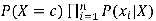
Cette règle de décision est appelée règle du maximum a posteriori.

Exemple d’application

Considérons des transactions bancaires, telles qu’elles peuvent apparaître sur un relevé de compte. Elles sont constituées :

d’une date
d’un descriptif court
d’une description longue
d’un montant

On cherche à classer automatiquement nos transactions en catégories prédéfinies. Nous choisirons ici les catégories (assez génériques) suivantes :

paiement
virement
frais de paiement
frais de virement
frais bancaires
régularisation

Constitution du jeu d’entraînement

Nous allons dans un premier temps prendre un extrait de relevé et classer chaque transaction dans une catégorie. Nous ne nous intéresserons qu’aux descriptions qui accompagnent les transactions, en considérant que les dates et les montants apportent plus de bruit que d’information dans le cadre de ce problème précis.

Voici un extrait de l’ensemble d’entraînement au format CSV où les catégories ont été renseignées dans le dernier champ (elles apparaissent ici codées par le mot en gras) : VIR RECU 854526,VIR RECU 8545269324 DE: OCTO TECHNOLOGY MOTIF: VIREMENT SALAIRES JUIN 11,**transfer** CARTE X2052 RETRAI,CARTE X2052 RETRAIT DAB 22/06 21H37 CIC PARIS SAINT ROCH 10859A00 ,**withdrawal** CARTE X2052 21/06 ,CARTE X2052 21/06 PHIE LA BOETIE ,**payment** OPTION TRANQUILLIT,OPTION TRANQUILLITE,**fees** COTISATION JAZZ,COTISATION JAZZ,**fees** FRAIS PAIEMENT HOR,FRAIS PAIEMENT HORS ZONE EURO 1 PAIEMENT A 1.00 EUR NT 38.06 EUR A 2.70,**atmfees** FRAIS PAIEMENT HOR,FRAIS PAIEMENT HORS ZONE EURO 1 PAIEMENT A 1.00 EUR NT 3.33 EUR A , **atmfees**

Modélisation des transactions

Nous allons utiliser un modèle de Bernoulli multivarié, dans lequel un fragment de texte est représenté par les occurrences des mots qu’il contient. Cette représentation s’appuie sur un dictionnaire ordonné, dont la construction est un préalable à l’apprentissage des paramètres du modèle.

Dans cet exemple, le dictionnaire a été constitué de mots apparaissant dans l’ensemble des transactions proposées, et la première ligne de notre jeu d’entraînement sera représentée de la manière suivante :


ANNUL	0	ANNULCARTE	0	BOETIE	0	CARTE	0	CIC
COTISATION	0	DAB	0	EUR	0	EURO	0	FRAIS
HAUSSMANN	0	HORFRAIS	0	HORS	0	JAZZCOTISATION	0	JAZZ
JUIN	1	MOTIF	1	OCTO	1	OPTION	0	PAIEMENT
PARIS	0	PHIE	0	RECU	1	RETRAICARTE	0	RETRAIT
ROCH	0	SAINT	0	SALAIRES	1	TECHNOLOGY	1	TRANQUILLITOPTION
TRANQUILLITE	0	VIR	1	VIREMENT	0	X2052	0	ZONE

Soit le vecteur (0,0,0,1,0,0,0,0,0,0,1,0,0,1,0,0,0,1,1,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0).

Remarque : Dans ce modèle, la fréquence des mots n’importe pas, non plus que leur ordre d’apparition. On ne tient compte que de leur occurrence. Le modèle multinomial utilise une approche légèrement différente pour construire un vecteur constitué des indices des mots dans le dictionnaire, et donc conservant l’ordre des mots du document original. Pour de petits documents, comme c’est le cas ici, les résultats seront peu ou prou équivalents. Pour des documents plus conséquents, le modèle multinomial donne en général de meilleurs résultats.

Préparation des données

Pour constituer le dictionnaire, on utilisera en pratique soit un corpus de termes préétabli et un lissage pour les termes qui n’apparaissent pas dans le corpus d’entraînement, soit l’ensemble de tous les termes trouvés dans les exemples. La deuxième solution garantit qu’aucun vecteur ne sera nul et que chaque caractéristique sera représentée mais elle limite le dictionnaire à l’ensemble des termes présents dans l’ensemble d’entraînement. La première solution, quant à elle, permet l’utilisation d’un plus grand nombre de termes, mais elle n’apporte pas d’information pertinente sur les termes non représentés (puisqu’elle leur associe une probabilité arbitraire). De plus, certains termes apportent essentiellement du « bruit ». Dans notre exemple, nous avons retiré les codes et caractères symboliques (parenthèses, ponctuation, chiffres) pour ne retenir que les « mots » à proprement parler. Pour maximiser la pertinence des termes retenus, il existe un bon nombre de techniques plus ou moins raffinées. Dans le domaine de la classification de texte, on trouve parmi les plus courantes :

la liste de « stop words ». Ce sont des mots qui ne convoient pas de sémantique, comme les pronoms ou les articles. Ils sont éminemment contextuels, et ils dépendent en particulier de la langue de rédaction.
Le « stemming », qui consiste à réduire les formes infléchies à un radical. Par exemple, « mangé », « manger », « mangeant » seront tous les trois réduits à « mange ». On évite ainsi la diffusion d’un même concept sur des caractéristiques différentes. Incidemment, cela permet de mitiger l’hypothèse d’indépendance en réduisant, par identification, le nombre total de caractéristiques.

Dans le cas qui nous préoccupe, nous avons choisi d’appliquer les transformations suivantes :

Elimination des caractères non alphabétiques
Restriction aux termes qui apparaissent au moins deux fois dans le corpus

Ces deux transformations permettent ici de retirer des codes de transaction qui contribuent à beaucoup de classes (et sont donc peu discriminants) et d’ignorer des termes spécifiques à une seule transaction (et qui du coup contribuent à discriminer artificiellement des transactions de même classe).

Implémentation

Weka

Pour construire notre classifieur, nous avons utilisé la librairie Weka, implémentée en Java. Weka est une librairie qui implémente sous une API relativement unifiée la plupart des algorithmes utilisés en apprentissage automatisé, pour la classification comme pour la régression. Elle n’est pas forcément la plus indiquée pour un usage en production (ne serait-ce que parce que son API est conçue pour une utilisation en ligne de commande et que sa gestion des exceptions est assez rudimentaire), mais l’étendue de sa couverture ainsi que son intégration à une interface graphique la rend particulièrement indiquée pour l’expérimentation. En particulier, elle permet de manière simple d’obtenir des statistiques sur le classifieur entraîné (erreur absolue et relative, individus correctement classés…) qui sont précieuses dans un cadre expérimental.

Un peu de code…

Tout d’abord, nous allons construire un vecteur à partir de notre document, soit ici la description de la transaction. Pour cela, nous avons choisi d’implémenter une classe dédiée, qui se charge de la construction incrémentale du dictionnaire (les imports ont été omis). Cette classe va dans un premier temps ajouter des mots au dictionnaire à partir du moment où ils apparaissent au minimum deux fois (méthode initialize). Dans un second temps, elle va renvoyer un vecteur indicé d’après le dictionnaire ainsi construit à partir d’un fragment de texte (méthode vectorize).

package aga.weka.naive;

public class TextVectorizer {
	// rassemble les mots du corpus d’entraînement
	private List<String> dictionary = null;
	private Attribute classAttribute;
	private FastVector allAttributes = null;
	
	// Cette méthode construit le dictionnaire à partir
	// de tous les mots présents au moins deux fois dans
	// la chaîne doc passée en paramètre et les ajoute à
	// la liste dictionary.
	public void initialize(String doc, Attribute classAttr) {
		...
	}


	// Cette méthode prend un document en paramètre et 
	// renvoie une liste indicée d’après le dictionnaire,
	// dans laquelle un "1" indique la présence du mot
	// d’indice correspondant.
	public Instance vectorize(String doc) {
		...
	}
	
	public Attribute getClassAttribute(String name) {
		return classAttribute;
	}
	
	
	public FastVector getAttributes() {
		return allAttributes;
	}
}

Maintenant, à partir de notre ensemble d’entraînement préalablement constitué sous forme de fichier CSV et de la forme « description, classe », nous allons construire un classifieur bayésien en utilisant l’implémentation de Weka :

package aga.weka.naive;

public class TextCat {
	private static final String DATA_DIR 
	  = " /eclispe-wkspc/ml/weka-naivebayes/datasets";
	private static final String TRAINING_FILE
	  = DATA_DIR + "/training-text.csv";
	private static final String TEST_FILE
	  = DATA_DIR + "/testing-text.csv";
	private static final String DATASET
	  =  DATA_DIR + "/full-20110819.csv";

	// le libellé de transaction apparaît en
	// en premier dans le fichier CSV :
	private static final int DOC_IDX = 0;

	// et la classe en seconde position :
	private static final int CLASS_IDX = 1;

	private static TextVectorizer vectorizer
	  = new TextVectorizer();

	/**
	 * @param fileName    Path to a CSV file with the samples
	 * @param classIndex  Index of the class attribute
	 * @return A dataset containing the data from the file
	 * 
	 * @throws Exception (from the Weka API... sucks...)
	 */
	private static Instances getDataSetFromFile(
	  String fileName,
	  int classIndex
	) throws Exception {
		// utilitaire de lecture de notre fichier CSV
		CSVLoader loader = new CSVLoader();
		loader.setFile(new File(fileName));
		
		Instances dataset = loader.getDataSet();
		// précise quel champ représente la classe
		dataset.setClassIndex(classIndex);
		
		return dataset;
	}
	

	/**
	 * Takes in a dataset and, given the index of the 
	 * text feature, outputs a feature vector indexed
	 * against the dictionary previously initialized.
	 * 
	 * @param dataset  The dataset to vectorize
	 * @param docAttr  The index of the text feature
	 * @param name     Name of the target dataset
	 * 
	 * @return  Dataset containing feature vectors
	 *          for the input dataset
	 * 
	 * @see #vectorizer
	 */
	private static Instances vectorize(
	  Instances dataset, 
	  int docAttr, String name
	) {
		Instances vectors
		  = new Instances(
				name, 
				vectorizer.getAttributes(), 
				dataset.numInstances()
		    );

		vectors.setClass(vectorizer.getClassAttribute(null));
		vectors.setClassIndex(vectors.numAttributes()-1);

		Enumeration<Instance> i
		  = dataset.enumerateInstances();

		while (i.hasMoreElements()) {
			Instance instance = i.nextElement();
			Instance vector
			  = vectorizer.vectorize(
			      instance.stringValue(docAttr)
			    );
			vectors.add(vector);
		}
		
		i = dataset.enumerateInstances();
		Enumeration<Instance> v
		  = vectors.enumerateInstances();

		while (i.hasMoreElements()) {
			Instance instance = i.nextElement();
			Instance vector = v.nextElement();

			// déterminer la classe si elle est fournie
			if (!instance.classIsMissing()) {
				int cidx = instance.classIndex();
				String classValue
				  = instance.stringValue(cidx);

				if (classValue != null
				    && !classValue.equals("")
				) {
					vector.setClassValue(classValue);
				}
			}
		}
		return vectors;
	}

	/**
	 * @param args  CL arguments
	 * @throws Exception (the Weka API leaking again...)
	 */
	public static void main(String[] args) throws Exception {
		Instances trainingSet
		  = getDataSetFromFile(TRAINING_FILE, CLASS_IDX);

		/*
		 * Initialise le vectorizer utilisé par la suite 
		 * pour vectoriser les échantillons de test et
		 * d'entraînement. 
		 * Ceci initialise en parallèle le dictionnaire
		 * utilisé pour représenter les transactions.
		 */
		Enumeration<Instance> e
		  = trainingSet.enumerateInstances();
		
		StringBuilder words = new StringBuilder();
		while (e.hasMoreElements()) {
			words.append(' ')
			     .append(e.nextElement().attribute(DOC_IDX));
		}
		vectorizer.initialize(
		  words.toString(),
		  trainingSet.classAttribute()
		);
		
		Instances trainingVectors
		  = vectorize(
		      getDataSetFromFile(TRAINING_FILE, CLASS_IDX),
		      DOC_IDX, "training"
		    );
		
		// entraîner le modèle avec les exemples :	
		Classifier model = new NaiveBayes() ;
			
		model.buildClassifier(trainingVectors);
			
		// évaluer le modèle avec le fichier de test :
		Instances testingVectors
		  = vectorize(
			getDataSetFromFile(TEST_FILE, CLASS_IDX),
			DOC_IDX,
			"testing"
		    );
		
		Evaluation eval = new Evaluation(trainingVectors);
		eval.evaluateModel(model, trainingVectors);
	
		// afficher les indicateurs du modèle entraîné :
		System.out.println(eval.toSummaryString());
			
		// essayer de catégoriser de nouvelles transactions :
		Instances dataset = getDataSetFromFile(DATASET, 4);
		Instances vectors = vectorize(dataset, 2, "samples");

		Enumeration<Instance>
		  i = dataset.enumerateInstances();

		Enumeration<Instance>
		  v = vectors.enumerateInstances();

		while (i.hasMoreElements()) {
		  Instance instance = i.nextElement();
		  Instance vector = v.nextElement();
		  if (!instance.classIsMissing()) continue;
		  double prediction = model.classifyInstance(vector);
		  int classIdx = (int)Math.round(prediction);
		  String detail = instance.stringValue(2);
		  
		  String clazz 
		    = vectors.classAttribute().value(classIdx);

		  System.out.println(
		    prediction + "(" + clazz + ") - " + detail
		  );
		}
	}
	
}

Test

Pour tester notre classifieur, nous avons simplement exécuté ce programme sur un relevé bancaire fraîchement téléchargé auquel nous avons fait subir les mêmes transformations qu’à l’ensemble d’entraînement, c’est-à-dire :

Ne retenir que la description de la transaction
Eliminer les caractères non alphabétiques
Catégoriser manuellement chaque transaction

Voici un extrait de la sortie de notre programme de test :

Correctly Classified Instances 229 94.6281 % Incorrectly Classified Instances 13 5.3719 % Kappa statistic 0.9238 Mean absolute error 0.0107 Root mean squared error 0.1037 Relative absolute error 7.6116 % Root relative squared error 39.2315 % Coverage of cases (0.95 level) 94.6281 % Mean rel. region size (0.95 level) 10 % Total Number of Instances 242

6.0(fees) - OPTION TRANQUILLITE
6.0(fees) - COTISATION JAZZ
0.0(transfer) - PRELEVEMENT 4871600969 TRESOR PUBLIC 75 MENM275026474023071 750710504383389328 111
1.0(withdrawal) - CARTE X2052 RETRAIT DAB 17/08 04H03 HSBC FRANCE MONTMARTRE 771031
1.0(withdrawal) - CARTE X2052 RETRAIT DAB 16/08 12H50 DAB DE LA BANQUE POSTALE 756451
2.0(payment) - CARTE X2052 16/08 COCCI MARKET
... 3.0(regularisation) - REGULARISATION DE COMMISSION FRAIS RET EUR DAB UE HORS SG DU MOIS DE JUILLET 2011 1 RETRAIT A 1.00 EUR NT 4.0(atmfees) - FRAIS RET EUR DAB UE HORS SG CARTE 4973019651342052 11 RETRAITS EN 07/2011 FORFAIT MENS 5.0(transferfees) - FRAIS SUR VIREMENT PERMANENT DU 28/07/11
0.0(transfer) - PRELEVEMENT 3269732986 BOUYGUES TELECOM PAGP01008RO2TM *418323
1.0(withdrawal) - CARTE X2052 RETRAIT DAB 30/07 03H09 BANQUE DE FRANCE 00010006
... 4.0(atmfees) - FRAIS RET EUR DAB UE HORS SG CARTE 4973019651342052 11 RETRAITS EN 06/2011 FORFAIT MENS 1.0(withdrawal) - CARTE X2052 RETRAIT DAB 30/06 00H57 DAB DE LA BANQUE POSTALE 757171
5.0(transferfees) - FRAIS SUR VIREMENT PERMANENT DU 28/06/11
... 9.0(regul) - REGULARISATION SUR CARTE X8463 PAIEMENT FRANCE 110111200666161 20/04/11 AIR FRANCE
9.0(regul) - REGULARISATION SUR CARTE X8463 PAIEMENT FRANCE 110111100096286 19/04/11 FINDMYORDER.COM
... 8.0(payfees) - FRAIS PAIEMENT HORS ZONE EURO 1 PAIEMENT A 1.00 EUR NT 3.39 EUR A 2.70
8.0(payfees) - FRAIS PAIEMENT HORS ZONE EURO 1 PAIEMENT A 1.00 EUR NT 16.89 EUR A 2.70
4.0(atmfees) - FRAIS RETRAIT HORS ZONE EURO 1 RETRAIT A 3.00 EUR NT 62.53 EUR A 2.70
4.0(atmfees) - FRAIS RETRAIT HORS ZONE EURO 1 RETRAIT A 3.00 EUR NT 81.29 EUR A 2.70
... 6.0(fees) - OPTION TRANQUILLITE
6.0(fees) - COTISATION JAZZ
...

La première partie nous indique comment notre classifieur s’est comporté vis-à-vis de notre ensemble de test. Les indicateurs intéressants sont les suivants :

La proportions d’individus correctement classés (ici 94,6 %)
L’erreur relative (ici 7,6%)

Cela signifie concrètement que, sur notre ensemble de test, le classifieur entraîné sur nos exemples a correctement classé près de 95% des transactions qui lui ont été présentées (ce très bon score est en bonne partie dû à la faible variance des exemples et au petit nombre de classes). L’erreur relative est utile quant à elle pour comparer les performances de plusieurs classifieurs sur un même jeu d’entraînement/test.

Conclusion

Nous avons implémenté un embryon de gestionnaire de finances personnelles, ou tout du moins la partie le constituant qui permet de catégoriser des dépenses (sur des catégories très simples, il est vrai). Pour cela, nous avons utilisé un des classifieurs les plus simples existant, mais qui donne de bon résultats pour des volumes réduits d’exemples : ici, nous atteignons (sur la base d’un ensemble d’entraînement de quelques centaines d’individus), un taux de classification correcte de près de 95%.

Les classifieurs de Bayes se révèlent en pratique bien adaptés aux problèmes de catégorisation de texte, et ont l’avantage d’être extrêmement économes en puissance de traitement, du fait même de l’hypothèse d’indépendance qui les fonde (la loi de distribution de chaque caractéristique pouvant alors être exprimée indépendamment des autres en une seule dimension au lieu d’un nombre de dimensions en puissance du nombre de caractéristiques, qui pave la route au « fléau de la dimensionnalité », caractérisé notamment par le fait qu’un nombre exponentiel d’exemples est requis en l’absence d’une telle hypothèse pour aboutir à une performance identique). Cet exemple « jouet » nous a permis de les évaluer dans une situation concrète.

Pour aller plus loin...

Voici quelques références pour creuser le sujet : L’incontournable article de Wikipedia Une lecture d’Andrew Ng, avec un passage sur les classifieurs de Bayes La justification au paradoxe apparent de la performance de ces classifieurs Un pointeur vers des librairies open source d’apprentissage automatisé