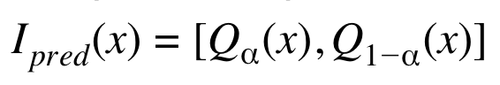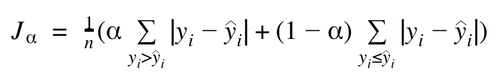Quantifier l’incertitude avec Random Forest : analyse et applications

le 09/11/2018 par Samuel Rochette

Dans le cadre de l’apprentissage supervisé, un modèle de régression permet d’inférer la valeur associée à une observation à partir d’exemples. Prosaïquement, on cherche à prédire le comportement moyen d’une variable cible Y à partir des variables explicatives X décrivant les observations. C’est l'espérance de Y sachant X, notée E[Y|X].

Est-il possible d’aller chercher plus d’information que le seul comportement moyen à partir d’un modèle de prédiction ? Peut-on quantifier l’erreur de notre modèle dans ses prédictions ?

Pour illustrer la réponse à ces questions à l’aide d’exemples, on utilisera les données Superconductivty Data [1] recensant la température critique en Kelvin en dessous de laquelle différents matériaux deviennent supraconducteurs. La variable cible Y est ici la température critique (critical_temp). Les variables explicatives X définissent la structure atomique du matériau.

Figure 1 : Echantillon des données Superconductivty Data

Il convient de ne pas confondre intervalle de prédiction et intervalle de confiance (le second donne un intervalle pour la moyenne conditionnelle, prenant en compte seulement l’erreur due à l'échantillonnage, tandis que le premier prend en plus en compte l’erreur du modèle par rapport à la valeur réelle)

Random Forest, d’une prédiction à une distribution

L’algorithme Random Forest [2] est un agrégat d’« apprentisseurs faibles ». En d’autres termes, on construit de nombreux modèles simples (ici, des arbres de décision binaire). La prédiction globale de l’algorithme est donnée en prenant la moyenne des prédictions de chaque arbre.

Un arbre de décision binaire en régression est construit avec des noeuds (représentant des règles) sur les variables explicatives. Par exemple, la masse atomique moyenne de l’observation est-elle inférieure à 60u ?

Ces règles sont automatiquement définies en minimisant une fonction de coût J. On minimise J en calculant sa valeur sur différents seuils de différentes variables. Par défaut, la librairie scikit-learn implémente la mean squared error (moyenne des erreurs au carré) : 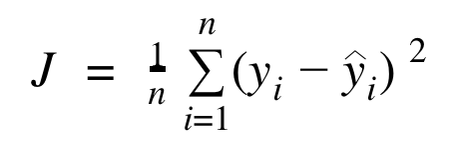C’est la minimisation de cette fonction de coût qui donne l’estimation de la moyenne conditionnelle.

import os from sklearn.ensemble import RandomForestRegressor from sklearn.tree import export_graphviz from IPython.display import Image rf = RandomForestRegressor(criterion='mse', n_estimators=1000, min_samples_leaf=1) rf.fit(X_train, y_train) export_graphviz(rf.estimators_[0], out_file='tree_superconduct.dot', feature_names=X_train.columns, max_depth=1, precision=0, filled=True, rotate=True, rounded=True) os.system('dot -Tpng tree_superconduct.dot -o tree_superconduct.png') Image(filename = 'tree_superconduct.png')

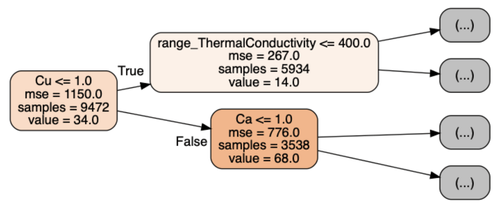
Figure 2 : Premiers noeuds du premier arbre de la forêt

La figure 2 illustre les trois premiers noeuds du premier arbre de régression :

chaque noeud est associé à une règle sur l’une des variables explicatives : Cu ≤ 1.0
mse est la valeur de l’erreur, on voit qu’elle diminue lorsqu’on avance dans l’arbre.
samples est le nombre d’observation passant dans le noeud, on vérifie que 5934+3538 donne bien le nombre d’observations initiales de cet arbre : 9472.
value est la moyenne des températures critiques des observations passant dans le noeud (i. e. la prédiction pour ce noeud).

Figure 3 : Premier arbre de la forêt

En réalité, un arbre de décision est par défaut construit jusqu’à ce que ses feuilles soient pures (i.e. contiennent une unique observation ou bien plusieurs observation ayant la même valeur de température critique). Cela correspond au paramètre min_samples_leaf=1.

Avec cette stratégie, on a l’information de la distribution des prédictions de chacun des arbres. En effet, pour une nouvelle observation, on peut récupérer les prédictions de chacun des 1000 arbres au lieu de ne garder que la valeur moyenne. Le nombre d’arbre est défini par le paramètre n_estimators.

On obtient ainsi une estimation de la distribution conditionnelle, définie par sa fonction de répartition : qui associe pour y ∈ R la probabilité pour une observation x donnée que sa réponse Y soit inférieure à y :

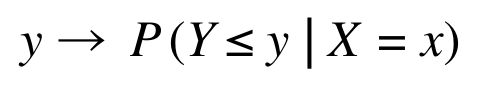
 decision_tree_predictions_matrix = [[decision_tree.predict(np.array([X_test.iloc[i]]))[0] for decision_tree in rf.estimators_] for i in range(len(X_test))] 

Cette ligne de code retourne la matrice des prédictions de chaque arbre pour chaque observation. Cette matrice nous permet ensuite de tracer la figure 4.

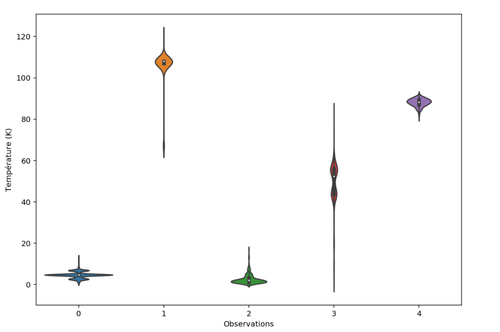
Figure 4 : Distribution des prédictions pour les matériaux 0 à 4

A partir de ces distributions conditionnelles par matériau, il est possible de calculer la moyenne (valeur retournée par la méthode predict de scikit-learn), mais aussi la médiane, les quantiles et d’autres moments statistiques.

Quantifier la confiance du modèle

Intéressons nous plus particulièrement aux quantiles de ces distributions. Ils permettent de construire les intervalles de prédiction pour chaque matériau x :

En prenant ɑ égale à 0.05, 1-ɑ vaut 0.95. Cela signifie qu’on sélectionne les 5ème et 95ème centiles dans la distribution prédite pour l’observation x.

Ces deux valeurs forment l’intervalle de prédiction 90 (i.e. l’intervalle qui a une probabilité 0.9 de contenir la vraie valeur mesurée de température critique pour le matériau).

 lower_bound_predictions = [np.percentile(prediction_distribution, 5) for prediction_distribution in decision_tree_predictions_matrix] upper_bound_predictions = [np.percentile(prediction_distribution, 95) for prediction_distribution in decision_tree_predictions_matrix] 

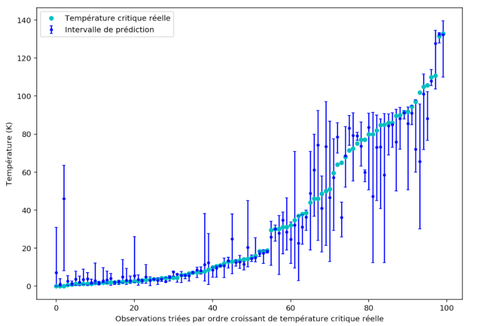
Figure 5 : Intervalles de prédiction 90 pour 100 observations

On peut vérifier qu’environ 90% des intervalles contiennent la valeur réelle de température critique :

 ground_truth_inside_interval = len([1 for i, value in enumerate(y_test) if lower_bound_predictions[i] <= value <= upper_bound_predictions[i]]) ground_truth_inside_interval_percentage = ground_truth_inside_interval / len(y_test) 

ground_truth_inside_interval_percentage vaut 0.87, ce qui veut dire que 87 intervalles sur les 100 contiennent la valeur mesurée de température critique sur la figure 5. Le résultat semble cohérent avec la probabilité 0.9 attendue.

On a ainsi la possibilité de quantifier à quel point le modèle est sûr de lui. Les petits intervalles de prédiction à gauche de la figure 5 illustrent que les centiles 5 et 95 sont proches l’un de l’autre car les « apprentisseurs faibles » sont d’accord entre eux et prédisent à peu près la même valeur. Le modèle est robuste pour ces observations. En revanche, pour les intervalles de droite, la variance semble bien plus élevée.

On intuite visuellement que les prédictions les plus éloignées de la valeur réelle de température critique sont entourées d’un grand intervalle. On peut vérifier cela en calculant le coefficient de corrélation entre l’erreur (de la moyenne conditionnelle) et la taille de l’intervalle.

 from scipy.stats.stats import pearsonr interval_length = upper_bound_predictions - lower_bound_predictions absolute_error = abs(y_test - rf.predict(X_test)) pearsonr(interval_length, absolute_error) 

On trouve une corrélation positive de 0.68 que l’on peut qualifier de forte car supérieure à 0.5 et significative car sa valeur associée de p est inférieur à 10-8.

Cette information est très utile pour le métier pour au moins trois raisons :

Dans un cas d’usage ou l’action à prendre est délicate (médecine, fraude, ...), on appréciera le fait de mesurer l’incertitude (pas d’action si l’intervalle de prédiction est trop grand).
Ces intervalles donnent une information riche sur les données utilisées pour l’entraînement. En effet, si un intervalle de prédiction est grand, on peut induire qu’il y a peu d’individus « proches » de celui-ci dans les données d’entraînement, ou bien que les individus « proches » ont des réponses très éparses. Dans les deux cas, il peut être judicieux - si possible - d’aller mesurer plus d’individus dans ces zones.
Un intervalle très grand peut enfin signaler une valeur aberrante dans les données d'entraînement ou une anomalie dans les données de test.

Généralisation

Faire croître les arbres jusqu’à ce que les feuilles soient pures (comme le suggère Breiman [2]) ne donne pas toujours des résultats optimums selon la métrique choisie. On peut ajuster le paramètre min_samples_leaf pour chercher de meilleurs résultats.

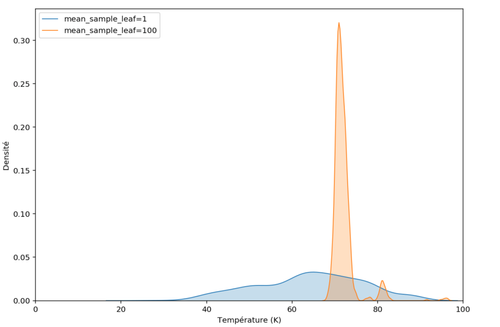
Réglons ce paramètre à 100 (les feuilles des arbres contiendront au minimum 100 observations) et étudions une distribution prédite pour une observation ayant une température critique réelle élevée de 70K.

Figure 6 : Comparaison des distributions prédites pour un matériau

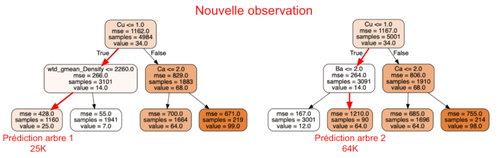
La distribution orange est moins large que la bleue, la variance a diminué. De fait, en limitant la taille des arbres, on ne garde que la valeur moyenne des températures critiques de matériaux qui tombent dans chaque feuille. On n’a plus la distribution complète des températures critiques qui ont servies à l’entraînement mais seulement une distribution de moyennes d’échantillons provenant de ces températures critiques.

Ainsi, lorsqu’on réitère la procédure de la figure 5, seulement 54 intervalles sur 100 contiennent les vraies valeurs de température critique. C’est très éloigné de la valeur attendue 90. Le résultat ne semble plus cohérent avec la probabilité 0.9 attendue.

On peut néanmoins pallier le problème en gardant en mémoire les valeurs de chaque observation dans les feuilles pour reconstruire la distribution des températures critiques observées lors de l’entraînement.

Figure 7 : Une feuille non pure

On voit dans cette feuille qu’il y a plus de 100 observations (samples) des données d’entraînement. Seule la température critique moyenne 32K est mémorisée. L’algorithme Quantile Regression Forest [3] propose de garder en mémoire le tableau des 103 températures critiques associées à cette feuille (et de même pour chaque feuille de chaque arbre) afin de reconstruire les distributions conditionnelles.

Pour chaque prédiction, on calcule la distribution en concaténant toutes les valeurs présentes dans les feuilles dans lesquelles cette prédiction termine.

Figure 8 : Prédictions dans une forêt à deux arbres de profondeur 2

Sur l’exemple simplifié de la figure 8, on construirait la distribution de la nouvelle observation avec les valeurs des observations d’entraînement des feuilles dans lesquels l’observation tombe. Ici, 1160 valeurs des données d’entraînement pour l’arbre 1 et 90 valeurs pour l’arbre 2.

Avec cet algorithme, la procédure de test de la figure 5 compte 92 intervalles qui contiennent la vraie température critique sur 100. Le résultat semble à nouveau cohérent avec la probabilité 0.9 attendue.

Conclusion

Une Random Forest délivre plus d’information qu’on ne le pense (surtout du point de vue métier) et on a vu dans cette article comment l'exploiter.
Ces informations sont : mesurer l’incertitude, connaître les éventuelles mesures supplémentaires à effectuer ou trouver des anomalies.
Attention cependant à ne pas chercher des intervalles de prédictions avec trop peu d’arbres (il faut un certain nombre de points pour décrire correctement les distributions).

Pour aller plus loin :

En classification, une probabilité est déjà un indicateur de confiance (cependant, peu d’algorithmes délivrent de vraies probabilités, il est souvent nécessaire de les calibrer)
La distribution de la variable cible Y peut avoir un impact sur les intervalles de prédiction. Ici, avec les températures en Kelvin minorées par zéro, la distribution est exponentielle. La variance des températures élevées est plus grandes, ce qui explique les intervalles plus grands à droite de la figure 5.
Une technique pouvant fonctionner indépendamment du modèle pour trouver les intervalles de prédiction est d’utiliser la fonction de coût quantile (plus lourd en calcul car valeur absolue non dérivable sur l'ensemble de son espace de définition : le calcul du gradient se fait de manière numérique et nécessite deux entraînements : un pour chaque centile) :

Références

[1] A data-driven statistical model for predicting the critical temperature of a superconductor, Kam Hamidieh. 2018

[2] Random Forest, Leo Breiman. 2001

[3] Quantile Regression Forests, Nicolai Meinshausen. 2006

[4] https://blog.datadive.net/prediction-intervals-for-random-forests/

[5] https://scikit-garden.github.io/examples/QuantileRegressionForests/