L’apprentissage par renforcement démystifié

le 20/02/2019 par Baptiste Saintot

L’apprentissage par renforcement (ou “reinforcement learning”) s’est imposé ces dernières années comme une thématique incontournable de la recherche en intelligence artificielle. Tout comme d’autres méthodes d’apprentissage automatique, les techniques de renforcement utilisées ne datent pas d’hier (l’algorithme de Q-learning a été introduit en 1989), mais se sont révélées aux yeux du monde grâce à des avancées emblématiques. C’est notamment grâce à un seul et unique programme de Q-learning, combiné avec de l’apprentissage profond (“deep learning”), que les ingénieurs de DeepMind ont atteint en 2014 des performances surhumaines à la quasi-totalité des jeux Atari, avant de battre une légende du jeu de Go deux ans plus tard.

Cet article ne vise pas à couvrir des problématiques avancées de l’apprentissage par renforcement, mais à en démystifier les concepts principaux à travers leur mise en application au sein d’un simple programme de Q-learning. Pour ce faire, nous utiliserons la librairie “gym” développée par l’organisation OpenAI et écrite en Python. Le code présenté dans cet article est disponible sur ce répertoire GitHub.

Les sujets couverts dans cet article :

Une description des principaux concepts de l’apprentissage par renforcement
La création d’un environnement à partir de la librairie gym d’OpenAI
Le décryptage d’un algorithme de Q-learning
Des pistes pour aller plus loin

Quelques rappels sur les notions de renforcement

Idée générale de l’apprentissage par renforcement

Un agent dans un état actuel S apprend de son environnement en interagissant avec ce dernier par le moyen d'actions. Suite à une action A, l’environnement retourne un nouvel état S’ et une récompense R associée, qui peut être positive ou négative.

Si cette description ne vous parait pas claire, illustrons ces principes avec un exemple du monde réel. Prenons par exemple un jeune enfant sachant à peine marcher et cherchant à atteindre un jouet dans une pièce. S’il se lève et qu’il se dirige vers le jouet en courant, il y arrivera plus rapidement que s’il y va en rampant. Cependant, il risque de se faire mal. Ainsi, le fait de s’en rapprocher rapidement lui apportera une récompense positive, mais s’il chute il recevra alors une récompense négative.

L’enfant va alors, par lui-même, apprendre à atteindre son jouet en évoluant dans son environnement et en cherchant à maximiser sa récompense. L’apprentissage par renforcement fonctionne de la même manière.

Mise en pratique : le jeu du Frozen Lake

Dans cette partie nous implémenterons un algorithme de Q-learning dont le but sera d’apprendre à un agent à jouer au Frozen Lake, un jeu disponible parmi les environnements OpenAI. L’objectif pour le détective OCTO, notre agent, est donc de partir d'une extrémité du lac gelé et d'arriver à l'autre sans tomber dans un trou, en empruntant si possible le chemin le plus court.

OpenAI et Gym

Gym est une librairie conçue en Python par l’organisation OpenAI. Elle est composée d’une collection d'environnements conçus pour tester et développer des algorithmes d’apprentissage par renforcement. Que ce soit pour s’initier à cette technique ou pour perfectionner ses algorithmes, gym permet à ses utilisateurs de se focaliser uniquement sur l’algorithmique et non sur la conception de l’environnement qui peut parfois s’avérer chronophage. Parmi les nombreux environnements disponibles, on retrouve des jeux (Taxi Driver, Frozen Lake, la suite Atari, etc.) mais aussi des simulations robotiques en 2D ou en 3D.

Maintenant, place à la pratique ! Avant de développer votre premier programme d’apprentissage par renforcement, vous devez commencer par installer la librairie gym, disponible sur le GitHub d’OpenAI.


pip install gym

Ensuite, ouvrez votre IDE Python préféré, importez gym et les autres librairies nécessaires : vous êtes désormais prêt à construire votre premier algorithme de Q-learning.


import gym
import numpy as np
import random
import time

from gym.envs.registration import register

Création de l’environnement

La première chose dont nous avons besoin dans le cadre de notre projet de renforcement avec gym est de créer un environnement avec lequel notre agent va interagir.

Notez que l’environnement par défaut du Frozen Lake implique un aléa sur l’exécution de l’action pour simuler une glissade sur la glace. Dans le contexte de ce tutoriel, on ne souhaite pas que l’agent “glisse”, d’où l’appel à la fonction register pour modifier ce paramètre.


register(
   id="FrozenLakeNotSlippery-v0",
   entry_point='gym.envs.toy_text:FrozenLakeEnv',
   kwargs={'map_name': '4x4', 'is_slippery': False},
)

env = gym.make("FrozenLakeNotSlippery-v0")

En fonction de l’environnement dans lequel un agent évolue, il existe deux types de tâches distinctes :

Continue : il n'y a pas d'état terminal. C’est le cas par exemple pour des placements boursiers.
Épisodique : il y a un point de départ et un ou plusieurs points d'arrivée (états terminaux) dans l'environnement. Un épisode correspond alors à une suite d'états, d'actions et de récompenses.

Dans le cas de notre jeu, il s’agit bien sûr de tâches épisodiques, où chaque épisode correspond à une partie qui se termine lorsque le joueur tombe dans un trou ou atteint l’extrémité opposée du lac.

Une des propriétés de notre environnement est le nombre d’états possibles. Le jeu se présente sous la forme d'un tableau de dimension 4x4 et l'agent peut évoluer dans chaque case de ce tableau, il y a donc 16 états possibles sur le lac.


state_size = env.observation_space.n

Dans cet environnement, notre agent doit choisir à chaque étape s’il souhaite se déplacer à gauche, à droite, en haut, ou en bas, ce qui nous donne un total de 4 actions disponibles.


action_size = env.action_space.n

L’algorithme de Q-learning

Le programme présenté implémente un algorithme de Q-learning. Ce dernier a pour objectif de déterminer une stratégie (ou “policy”) optimale, qui permettra à l’agent de choisir les actions qui le mèneront à la victoire : l’agent pourra alors choisir la meilleure action quel que soit l’état dans lequel il se trouve.

Création de la Q-table et initialisation des Q-values

Il est maintenant temps d’introduire un outil central à notre algorithme de Q-learning : la Q-table. Il s’agit d’une matrice qui stocke, pour chaque état, une valeur correspondant à la somme attendue des récompenses que chaque action nous reporterait. Cette matrice évoluera ensuite de manière itérative selon les valeurs prises par la fonction Q, que nous détaillerons plus tard.

Dans un premier temps, elle est initialisée à zéro puisque nous n’avons aucune connaissance de notre environnement, avec une ligne par état et une colonne par action.


Q_table = np.zeros((state_size, action_size))
rewards = []

Mise à jour itérative de la Q-table

Nous arrivons maintenant au coeur de notre algorithme de Q-learning. A travers de multiples parties, plus communément appelées “épisodes”, nous allons entraîner notre agent à évoluer sur le lac gelé. Nous pouvons commencer par définir ce nombre de parties explicitement.


MAX_EPISODES = 15000

Il est également nécessaire de choisir un pas d’apprentissage (“learning rate”) ɑ, que l’on retrouve dans de nombreux algorithmes d’apprentissage automatique et qui nous servira pour la mise à jour itérative de la Q-table.


ALPHA = 0.8
GAMMA = 0.95

Nous verrons un peu plus tard à quoi correspond la constante ɣ, ainsi que tous les paramètres ci-dessous liés à ε.


EPSILON = 1.0
MAX_EPSILON = 1.0
MIN_EPSILON = 0.01
DECAY_RATE = 0.005

Débute alors la boucle d’apprentissage par renforcement qui va, pour chaque épisode, réinitialiser l’environnement et le total des récompenses obtenues puis faire évoluer notre détective OCTO dans la partie. Notre agent commence par choisir une action, puis l’applique à l’environnement avant de mettre à jour la Q-table grâce aux informations obtenues.


for episode in range(MAX_EPISODES):

    S = env.reset()
    step = 0
    done = False
    total_rewards = 0

    while not done:
        # ETAPE 1
        if random.uniform(0, 1) < EPSILON:
            A = env.action_space.sample()
        else:
            A = np.argmax(Q_table[S, :])

        # ETAPE 2
        S_, R, done, info = take_action(A, S)

        # ETAPE 3
        q_predict = Q_table[S, A]
        if done:  # Si la partie est perdue ou gagnée, il n’y a pas d’état suivant
            q_target = R
        else:  # Sinon, on actualise et on continue
            q_target = R + GAMMA * np.max(Q_table[S_, :])
        Q_table[S, A] += ALPHA * (q_target - q_predict)

        S = S_
        total_rewards += R
 
        env.render()
        time.sleep(0.1)

    EPSILON = MIN_EPSILON + (MAX_EPSILON - MIN_EPSILON) * np.exp(-DECAY_RATE * episode)
    rewards.append(total_rewards)

(#1) Choix de l’action et équilibre exploration vs. exploitation

A chaque étape de sa progression dans la partie, notre agent doit commencer par choisir une action à effectuer dans son environnement.

L’un des concepts centraux du Q-learning est l’équilibre à trouver entre exploration et exploitation tout au long de l’entraînement du modèle. En effet, il est nécessaire que notre détective OCTO continue à explorer son environnement tout en utilisant l’intelligence accumulée dans la Q-table à mesure des épisodes. Pour se faire, nous mettrons en place une stratégie dite “epsilon greedy” (ou ε-greedy policy) : on tire aléatoirement un nombre dans l’intervalle [0, 1[. Si ce nombre est inférieur à ε, l’agent va explorer son environnement ; dans le cas contraire il va exploiter les informations de la Q-table.

Exploration

Elle consiste à faire exécuter à l’agent une action aléatoirement. Lors du premier épisode l’agent ne va faire qu’explorer, puisque ε vaut 1. L’agent ne connaît pas son environnement, il ne peut donc pas se baser sur les valeurs de la Q-table, toutes initialisées à 0.

Exploitation

Elle consiste à faire exécuter à l’agent l’action ayant la valeur maximale dans la Q-table pour l’état actuel : le choix de l’action est donc basé sur l’exploitation de l’expérience emmagasinée par l’agent. Dans le cadre du Q-learning, les valeurs stockées dans la Q-table sont les valeurs prises par la fonction Q et correspondent à la somme des récompenses à attendre dans le futur pour chaque couple état-action.

L’agent cherche une stratégie (ou “policy”) optimale π*(s)=a, qui pour un état donné, va lui retourner l’action rapportant le plus de récompenses à terme. Après convergence, l’algorithme de Q-learning fournit donc une stratégie optimale π*(s) en choisissant l’action qui maximise la fonction Q dans un état donné :

π*(s) = argmax max__a Q*(s, a)

A la fin de chaque épisode, la valeur de ε est réduite, favorisant de plus en plus l’exploitation. Maintenir l’exploration à un niveau minimum permet toutefois à l’agent de continuer à s’entraîner en testant de nouvelles possibilités de jeu et éviter ainsi de rester coincé dans un optimum local.

(#2) Application de l’action dans l’environnement et récompense

L’action définie est alors appliquée à l’environnement via sa méthode step(action) (dans la fonction take_action). L’environnement se trouve pour l’instant dans un état S. Ce dernier nous retourne le nouvel état S’, ainsi qu’une récompense R. Ces feedbacks de l’environnement sont une étape clé du renforcement : ils nous permettront ensuite de mettre à jour notre Q-table.


def take_action(action, env):
    new_state, reward, done, info = env.step(action)
    # Fonction de récompense
    # Si new_state est un trou
    if new_state in [5, 7, 11, 12]:
        reward = -1
    # Sinon si new_state est l’arrivée
    elif new_state == 15:
        reward = 1
    # Sinon on pénalise la recherche
    else:
        reward = -0.01
    return new_state, reward, done, info

Dans le cas de l’environnement du Frozen Lake, le détective OCTO évolue case par case et les trous dans la glace ne bougent pas. Les récompenses sont définies de la manière suivante :

-1 lorsque notre agent tombe dans un trou sur le lac gelé (état terminal)
1 lorsque notre agent atteint l’autre côté du lac (état terminal)
-0.01 à chaque étape de notre agent : une méthode classique pour encourager l’agent à trouver le chemin le plus court parmi ceux qui lui permettent d’atteindre l’objectif final.

Notez que l’objectif de notre agent est de maximiser la somme des récompenses à venir, et non pas sa seule récompense de la prochaine étape. Ce dernier peut cependant décider d’accorder plus ou moins d’importance aux récompenses sur le long-terme, c’est ce que nous allons voir.

(#3) Mise à jour de la Q-table : l’équation de Bellman

Il est maintenant temps de modifier notre Q-table grâce aux informations reçues de l’environnement. Nous pouvons changer la valeur de la table pour l’action choisie dans l’état précédent. Cette mise à jour se fait grâce à l’équation de Bellman en utilisant notamment la récompense obtenue et un facteur d’actualisation, ɣ.

Sans rentrer dans les détails, l’intuition derrière ɣ est de permettre d’appliquer un discount aux récompenses attendues sur le long terme. Le plus souvent, on décide d’accorder une valeur plus élevée aux récompenses à court-terme, en considérant que ces dernières sont davantage prévisibles. Ainsi, dans le calcul de la valeur à indiquer dans la Q-table :

Plus ɣ est grand, plus on accorde d'importance au futur, donc aux récompenses sur le long terme.
Plus ɣ est petit, plus on accorde d'importance aux récompenses à plus court terme.

Suite à la mise à jour de la Q-table, il nous reste alors seulement à ajouter notre récompense au total des récompenses obtenues pendant cet épisode, et à faire du “nouvel état” l’état de départ de la prochaine boucle. A mesure des épisodes, l’algorithme va donc converger vers une Q-table optimale qui permettra de choisir une action pour chaque état.

Pour aller plus loin

“Policy-based” vs. “value-based”

Il existe plusieurs type d’approches d’apprentissage par renforcement. Dans l’exemple du Frozen Lake, nous avons vu que notre algorithme choisissait explicitement l’action associée à la valeur maximale de la Q-table pour un état donné : il s’agit de “value-based” Q-learning.

Une autre approche consiste à déterminer directement une stratégie (“policy”) optimale, sans expliciter de valeur associée à chaque action. Ainsi chaque état est directement associé à la meilleure action possible lui correspondant. Dans l’analogie de l’enfant utilisée précédemment, il s’agirait de son “instinct”, qui lui permet de choisir une direction sans comparer explicitement des valeurs.

Et le deep Q-learning dans tout ça ?

Imaginons maintenant qu’au lieu de jouer à un simple Frozen Lake, notre agent évolue dans un environnement bien plus complexe, caractérisé par une multitude d’états possibles. On peut par exemple s’imaginer une grille de jeu de 50x50, avec des ours blancs en mouvement cherchant à dévorer notre détective à la place de simples trous dans la banquise.

Si nous devions utiliser une Q-table pour choisir une action en fonction d’un état, nous aurions besoin de créer une matrice immense, car il y aurait autant de lignes dans la matrice que de valeurs différentes prises par chacun des descripteurs de l’état. Pour s’affranchir de ce problème, on peut entraîner un réseau de neurones qui, en fonction du large ensemble de descripteurs de l’état actuel, se chargera de déterminer la valeur associée à chaque action.

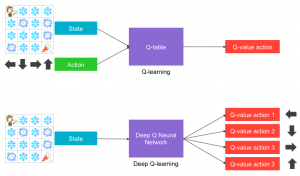
Dans le cas du deep Q-learning, le réseau de neurones fera donc office de Q-table en renvoyant une action à suivre pour chaque état. Le fitting du réseau pose cependant quelques challenges, que nous développerons dans un prochain article.

Conclusion

Nous avons terminé ce premier plongeon dans le monde de l’apprentissage par renforcement ! Maintenant que nous avons décrypté ensemble quelques grands concepts, vous êtes désormais prêt à aller plus loin. Vous pouvez d’ailleurs commencer par modifier les paramètres de votre algorithme de Q-learning, afin d’essayer d’en améliorer les performances.

Il est nécessaire de maîtriser les quelques concepts discutés avant d’explorer des techniques de renforcement plus pointues. Même si l’idée générale reste la même, les implémentations de renforcement plus complexes vont souvent de pair avec de nouvelles problématiques.

Les algorithmes de Q-learning peuvent rapidement devenir plus opaques : il devient alors difficile d’évaluer l’impact de chaque paramètre et d’expliquer les décisions prises par un agent. Le 37eme mouvement effectué par AlphaGo lors du second match contre le champion de Go Lee Seedol en est un parfait exemple. En effet, l’agent a choisi une action qui, en premier lieu, avait paru improbable et avait laissé perplexe tous les experts du jeu... avant de s’avérer prodigieuse et de permettre à AlphaGo de gagner la partie.

D’autre part, chaque application d’apprentissage par renforcement recèle également d’enjeux liés à l’environnement. S’il est simple de créer un environnement OpenAI, en pratique l’agent n’évolue pas toujours dans un jeu avec des règles bien strictes et définies : les contours du problèmes et caractéristiques de l’environnement ne sont pas toujours totalement maîtrisés. Simuler un environnement d’entraînement peut donc être un réel challenge, qu’il est nécessaire de surmonter pour pouvoir utiliser ces techniques.