Jumeaux Numériques Systémiques : modélisation des processus industriels et des activités
Introduction
Le Roy est mort. Vive le Roy !
Deux phrases. Un point.
Deux états. Une transition.
En traçant plusieurs dimensions de pouvoirs séculiers, spirituels, militaires ou économiques par des événements de transition entre états, un livre d’histoire propose les mêmes fonctionnalités que les Jumeaux Numériques Systémiques.
Le produit est conforme. Vive le produit !
Mais s’il y a non-conformité, quelle est la source du problème ?
Si le premier cas satisfait le jumeau physique, le second est plus intéressant à étudier dans son jumeau numérique. Il en va de même pour les livres d'histoires avec une guerre de 100 ans plus épique qu’un lénifiant “Le roi Louis XV meurt le 10 mai 1774. Le roi Louis XVI lui succède”. Les Rois Maudits passent mieux qu’un indigeste Malet-Isaac [1].
Pour comprendre comment ils deviennent les livres d’histoire des activités industrielles, ouvrons le capot des jumeaux numérique systémiques.
Contexte
Les Jumeaux Numériques des Processus suscitent un intérêt croissant chez les industriels, les centres de recherche et les collectivités territoriales soucieuses de gérer des systèmes physiques complexes.
La définition proposée par l'Alliance Industrie du Futur [2] des Jumeaux Numériques de Processus. est :
- Un ensemble organisé de modèles numériques représentant une entité du monde réel pour répondre à des problématique et des usages spécifiques ;
- Mis à jour par rapport au réel, à une fréquence et à une précision adaptées à ses problématiques et à ses usages ;
- Doté d’outils d’exploitation avancés permettant d’optimiser le fonctionnement et le pilotage de l’entité réelle.
Le CEA propose le concept de Jumeau Numérique Holistique [3] qui, de la conception à la production, intègre toutes les activités industrielles.
Entre les deux, les Jumeaux Numériques Systémiques (JNS) ont pour objectif de représenter une entité composite du monde réel dans un espace multidimensionnel.
Une dimension représentant un composant de l’entité globale, l'adjectif systémique implique la prise en compte de leurs interactions mutuelles.
Les Livres Blancs Culture Data et Industrie [4-5] détaillent comment modéliser un JNS par l’assemblage d’instances d’un unique objet : l’activité.
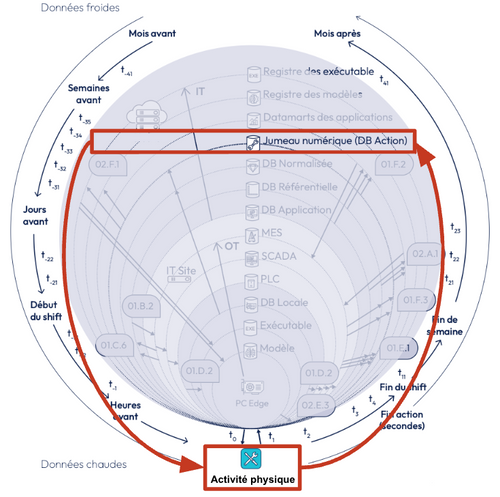
Le cycle de vie de la data Fig_1 illustre les interactions entre une entité composite, en l’occurrence une unité industrielle, et son JNS.
Fig_1 : Cycle entre l’activité physique et son jumeau numérique [4]
Note : les figures sont compressées, cliquer dessus pour les visualiser en haute définition
Les premiers Jumeaux Numériques de processus se sont focalisés sur la dimension Équipement qui est statiquement liée à une activité et connecté à de nombreuses sources de données (MES, FDC, etc.). Les applications de maintenance prédictive sont un exemple emblématique d’application outillant un jumeau numérique pour le pilotage d’un équipement.
Plus complexe, la dimension Produit est impliquée dans un grand nombre d’activités, ce qui la rend dynamique. À chacune d’entre elles, son identification logique requiert de nombreux systèmes (ERP, MES, etc.). La construction de son jumeau numérique nécessite la consolidation de données provenant de la dimension Équipement, parfois associées à un Id physique (RFID, QRcode, etc.) si la dimension Produit en est équipée.
C’est sur ces deux dimensions qu’ont historiquement été concentrés les efforts de pilotage process et lean avec les systèmes de collecte d’information associés.
Inversement, les activités non-productives (affutage, nettoyage, logistique interne, etc.) souffrent d’un manque qualitatif et quantitatif de données. Chronophage et rébarbative, la saisie des informations de ces activités à faible valeur unitaire perçue est souvent négligée et leur exécution manuelle est source d’erreurs humaines et d’écarts entre le planifié et le réel.
En conséquence de ces manques de données, les jumeaux numériques actuels ne permettent pas une analyse complète et en profondeur de la réalité concrète des processus industriels. Ils ne permettent donc pas de travailler sur l'efficacité de bout en bout de ces processus.
Exécutées en temps masqué, ces activités constituent la partie immergée de l’iceberg et prennent seulement la lumière lorsque l’une d’entre elles prend du retard. Tâches de support, leur rôle est la préparation des dimensions requises par les activités productives qui ne peuvent démarrer si une seule manque à l’appel (Qualification, Outil, Consommable, etc.).
C’est pour cela qu’une des principales propositions de valeur des JNS est l’optimisation du pilotage de la production par la connaissance multidimensionnelle des flux productifs et non-productifs.
Pour pallier à ces problèmes, les JNS doivent passer d’une logique de construction à partir des données disponibles à une logique plus ambitieuse de modélisation préalable des activités poursuivant plusieurs objectifs :
- Pour chaque activité :
- Cartographier l’espace à N dimensions en interaction (Équipement, Produit, Outil, Consommables, …) ;
- Répertorier les données et information produites ;
- Identifier le cas échéant les données supplémentaires à collecter. Cela peut passer par de nouveaux capteurs ou de nouvelles organisations.
- Pour chaque dimension :
- Établir la nomenclature des états possibles ;
- Construire son enchaînement d’activités ;
- Maîtriser ses changements de nature : un produit semi-fini se transforme en produit fini, un outil usé se transforme en outil affûté, des consommables sont regroupés dans un emballage, etc.
Ces données référentielles fonctionnelles ont deux fonctions :
- Documenter et cartographier les processus pour identifier des points d’amélioration et des sources de données complémentaires ;
- Outiller un JNS avec le pilotage par la comparaison continue du process ainsi modélisé et des données collectées de façon opérationnelle
Modélisation des activités et transitions
Comme nous l’avons vu, le pilotage d’un processus de production via un Jumeau Numérique nécessite de modéliser ses activités en prenant particulièrement en compte :
- Les activités non productives ;
- Un nombre significatif de dimensions pré-requises par activités.
Pour cela, rappelons la définition du modèle d’activité [5] qui se définit par la règle des trois unités.
L’unité d’action est une organisation d'activités ordonnées autour d'une intention : par exemple écouter et regarder sont des actions alors qu'entendre et voir sont des activités.
Dans le cas d’une activité manufacturière, l’intention est la production de biens ou de services qui se décompose en une séquence d’activités.
L’unité de temps désigne l’espace de temps délimité par deux événements. Chacun de ces événements conditionne donc un changement d’unité d’action.
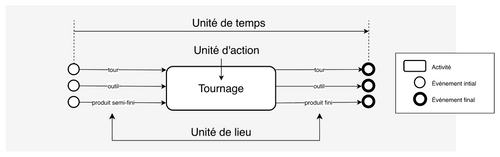
L’unité de lieu représente un espace à n dimensions. En l’occurrence, une dimension est un objet que l’on souhaite tracer : le produit fini, semi-fini, un équipement, un outil, etc.
Fig_2 : Modélisation de l’activité par la règle des trois unités
À l’inverse des états d’activité qui produisent des flux de données permettant de les instancier explicitement dans un jumeau numérique, les états de transition ne produisent pas d’informations. Par la donnée, il n’est possible d’instancier ces derniers que de façon implicite dans un intervalle entre deux activités. Par la modélisation, la connaissance a priori permet d’en contrôler la validité (“Est-il autorisé ?”, “Est-il absent ?”, “A-t-il été trop long ?”, etc.)
C’est pourquoi le modèle d’activités, productives et non-productives, doit être complété par celui des états de transitions entre celles-ci. Pour cela, introduisons leur annotation sémantique basée sur la construction syntaxique suivante “<Dimension> <Participe-passé> à <Infinitif>” :
- Dimension : avec précision d’état le cas échéant (ex : produit semi-fini, fini)
- Participe-passé : l’activité source, terminée
- Infinitif : l’activité cible, si celle-ci est connue
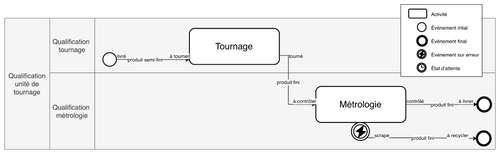
L’ajout de cette annotation sémantique localise et contextualise l’état de transition qui devient un objet à part entière. Sur Fig_3, il est ainsi possible de tracer une dimension juste par ses transitions :
- Produit semi-fini livré à tourner
- Produit fini tourné à contrôler
- Produit fini contrôlé à livrer
- Produit fini scrapé à recycler
En complément des activités, la connaissance de ces états de transition est nécessaire pour assurer un pilotage systémique des processus. Visualiser le nombre d’items par transition permet, par exemple, d’identifier les points de contention et de prioriser l’exécution des activités.
Ces représentations d’activités et de transitions étant posées, il reste à structurer leur assemblage en séquences. Pour cela, comparons quelques standards de modélisation industriels.
Modélisation systémique
La définition d’un Jumeau Numérique explicite le besoin d’un ensemble organisé de modèles numériques, en d’autres termes, il lui faut un modèle de données. Spécifiquement, pour un JNS, il faut un modèle systémique capable d'appréhender les relations entre tous types d’activités.
L’objectif est d’identifier le ou les standards de modélisation les plus adaptés aux contraintes du JNS.
Le Business Process Modeling Notation (BPMN) est le standard international qui prend le mieux en compte les processus événementiels multi acteurs. Cependant, comme le Value Stream Mapping (VSM), le Flowchart ou le Process Flow Diagram (PFD), il détaille principalement le cycle de vie de la dimension Produit. Sa structure multi acteurs permet également de distinguer la dimension qualification.
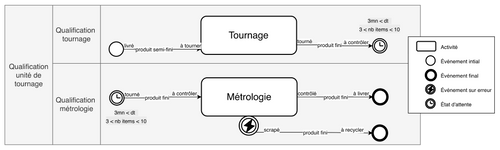
Prenons pour exemple la représentation d’une unité de tournage en Fig_3. Un BPMN très simplifié suit la chaîne de valeur qui la traverse et comporte deux activités réparties en fonction de la qualification des acteurs. Un BPMN plus complet multiplierait le nombre d’acteurs et d’activités mais le principe resterait le même avec des événements initiaux et de finaux qui délimitent la chaîne de valeur de la dimension Produit et des strates horizontales selon la dimension qualification.
Fig_3 : Modélisation BPMN simplifiée de l’unité
Si la dimension Produit a un cycle de vie pratiquement linéaire, d’autres dimensions ont des cycles de vie … cycliques. Nous allons voir que pour ces dernières ainsi que leurs activités non-productives associées, les MaE (Machines à États) sont plus adaptées à leur modélisation.
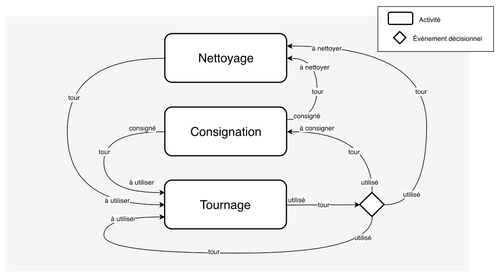
Fig_4 : MaE simplifiée de la dimension Équipement
La modélisation par MaE peut être contre-intuitive car sa représentation en graphe n’est ni spatiale, ni chronologique. Elle représente les transitions autorisées entre une liste finie d’états ou d’événements décisionnels. La particularité d’une transition pointant vers un événement décisionnel est d’ignorer l’activité cible (l’infinitif de la construction syntaxique).
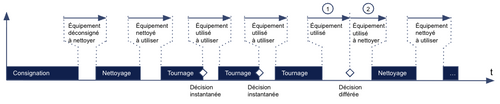
À la différence de la dimension Produit, la dimension Équipement n’a pas un cycle de vie linéaire. Sans événement initial ni final, elle peut enchaîner de façon cyclique plusieurs activités comme on peut le voir sur les instanciations chronologiques d’états en Fig_5 qui réitèrent plusieurs états d’activité et de transition. Si, à l’issue d’une activité la décision est instantanée, l’attente de celle-ci n’a plus lieu d’être et n’apparaît donc pas sur la chronologie.
Fig_5 : Chronologie des états pour la dimension Équipement
Jusqu’à présent, les BPMN nous ont permis de modéliser la dimension produit et les MaE les dimensions qui représentent la production (équipement, outil, consommable, etc.).
Pour intégrer dans un même modèle toutes ces dimensions, une solution simpliste pourrait être d’assembler directement Fig_3 et Fig_4 autour de l’activité de tournage.
Sur le principe, le schéma hybride contient toute l’information nécessaire à l’objectif d’un jumeau numérique systémique. Par exemple, pour connaître les causes racines possibles d’un produit fini scrapé, il est possible de remonter à l'activité de tournage. Si cette dernière n’est pas en cause, il est possible de remonter au :
- Produit semi-fini livré à tourner (Y a-t-il eu un problème de qualité du produit semi-fini en amont ?)
- Tour nettoyé à utiliser (l’activité de nettoyage a-t-elle été conforme ?)
- Tour consigné à utiliser (la consignation a-t-elle généré un problème ?)
- Tour utilisé à utiliser (Y a t-il eu un problème non détecté lors du précédent tournage ?)
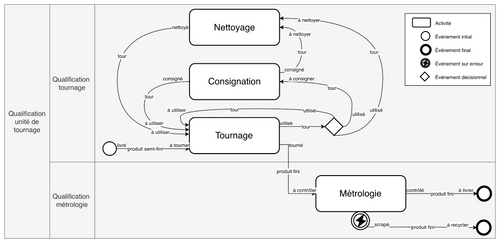
Fig_6 : Représentation hybride BPMN et MaE de l’unité de tournage
Au-delà de l’hétérogénéité de style, la prise en compte dans une machine à états de tous les états de transition pose un problème de complexité de la représentation graphique. Fig_6 représente seulement deux dimensions et quatre activités et deviendrait illisible s’il fallait représenter une unité de production comportant cinq dimensions et plusieurs dizaines d'activités.
Un autre problème, plus structurel, est d’avoir négligé jusqu’à présent la synchronisation des activités et les états d’attente. Pour cela, il faut distinguer les séquences continues de celles interruptibles.
Considérons une séquence comme une suite planifiée d’activités qui sont exécutées dans l'ordre, dans toutes les circonstances du traitement.
Une séquence continue implique une succession d’activités qui s’enchaînent en continuité. Dans ce contexte, la durée des transitions est perçue comme une perte de temps contrainte, qu'il faut réduire dans la mesure du possible.
Une séquence interruptible implique une discontinuité dans la succession d’activités. Celles-ci doivent s’exécuter dans l’ordre mais la séquence peut-être suspendue avant une reprise ultérieure. Dans ce cas, la transition est accompagnée du pictogramme État d’attente. L’annotation d’un état d’attente peut indiquer son caractère optionnel ou obligatoire par des règles sur le temps ou le nombre d’items partageant simultanément l’état.
Fig_7 : Séparation d’une séquence interruptible en deux continues
Si l’on considère que la séquence Fig_3 est interruptible, Fig_7 la sépare en deux séquences continues, graphiquement indépendantes tout en restant logiquement reliées par la transition répétée de part et d’autre du pictogramme État d’attente.
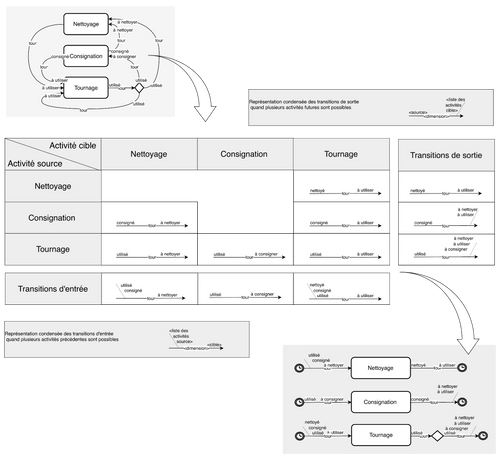
Fig_8 : Transformation de graphe par la matrice de transition entre états
L’aspect “Spaghetti” d’un graphe MaE n’est pas compatible avec celui du BPMN, plus largement adopté dans la culture industrielle. Pour en ramener l’information à l’échelle des activités comme en Fig_7, une matrice de transition entre états associée à une convention de représentation condensée des transitions permet de transformer une modélisation par Machine à États dans un formalisme BPMN (Fig_8).
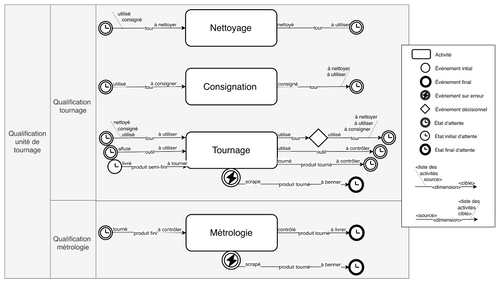
En appliquant ce principe, Fig_9 détaille les sous-activités et transitions de la qualification tournage de Fig_7. Cette représentation est beaucoup plus proche des préoccupations des acteurs opérationnels qui visualisent leurs activités par qualification. Cette liste d’activités est complétée par ce qui ressemble à une Bill Of Material (BOM) étendue. En effet, une BOM intègre les dimensions [produit, composant] mais pas [équipment, outil, consommable, qualification].
Fig_9 : Modélisation au niveau hiérarchique Unité
Le découpage des MaE permet la hiérarchisation de la modélisation à partir des contraintes fonctionnelles de synchronisation de séquences continues, exécutées par une ou plusieurs qualifications.
Il est ensuite possible de représenter un niveau hiérarchique inférieur d’une activité comme Tournage de Fig_9. Détaillée en cinq sous-activités, la séquence Fig_10 conserve les mêmes transitions en entrée et sortie, ce qui est requis pour des raisons de cohérence. Il en est de même pour Fig_11 qui correspond au niveau de hiérarchie supérieur qui intègre l’unité de tournage
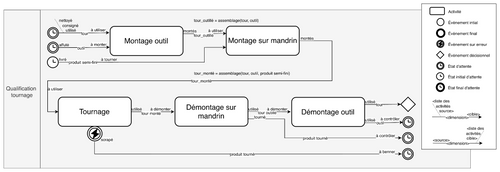
En fonction des spécificités fonctionnelles de l’activité, des dimensions résultant de l’assemblage temporaire de plusieurs d’entre elles, comme le montage d’un outil sur le tour ou d’une pièce sur le mandrin rendent celles-ci solidaires en une nouvelle dimension indissociable pendant une ou plusieurs activités. On obtient par exemple une dimension tour outillé = assemblage (tour, outil) (Fig_10)
Fig_10 : Modélisation au niveau hiérarchique Opération
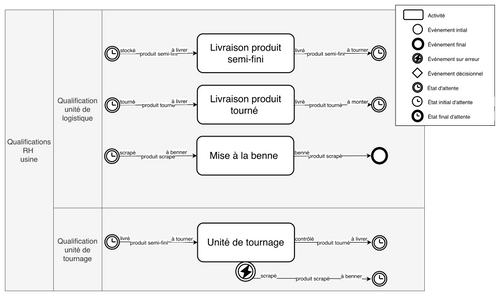
Fig_11 : Modélisation au niveau hiérarchique Site
Conclusion
L’état de l’art des Jumeaux Numériques des processus est focalisé sur les activités, c’est-à-dire les états qui produisent des données.
Les transitions entre celles-ci sont négligées jusqu’alors car non productrices de données.
Elles sont pourtant nécessaires à la modélisation d’un Jumeau Numérique Systémique qui intègre les interactions d’activités productives et non productives réparties sur plusieurs dimensions.
Pour cela, nous proposons un modèle systémique qui reprend les concepts des Machines à États adaptés au standard de modélisation BPMN.
Références
[1] : Malet-Issac : Livre d’histoire de l’enseignement secondaire au début du XXème , à la pédagogie délicieusement surannée
[2] : Jumeau Numérique Levier majeur de la transformation digitale de l’industrie -
www.https://solutionsindustriedufutur.org
[3] : The Holistic Digital Twin for Industry - Position paper on the Holistic Digital Twin for Industry Apr 27, 2024
[4] : Culture Data et Industrie, vol 2 page 101, Livre blanc Octo
[5] : Culture Data et Industrie, vol 1 page 9, Livre blanc Octo
https://publication.octo.com/culture-data-et-industrie-1