Introduction au calcul en grille pour l'évaluation de la Value At Risk

le 15/09/2010 par Marc Bojoly

La gestion des risques est aujourd'hui un objectif stratégique pour les institutions financières telles les banques d'investissement et les compagnies d'assurance. Une telle évaluation du risque utilise des mathématiques théoriques avancées et nécessite une grande puissance de calcul. Dans cet article, nous allons introduire les concepts de base de l'estimation de la Value At Risk de façon à montrer quel type de calcul est requis. Nous allons introduire le calcul en grille (grid computing) de façon à montrer de quelle façon une telle architecture peut aider les institutions financières à produire rapidement cet indicateur très important. Dans de futurs articles, nous décrirons en détail les implémentations de cet algorithme sur plusieurs intergiciels (middlewares) de calcul en grille.

Value At Risk

La Value At Risk est l'un des indicateurs de risque majeur pour les portefeuilles ou produits financiers. Elle a été introduite à la fin des années 1980 par les banques américaines (Banker's Trust puis J.P. Morgan). Elle donne une mesure de la perte maximale possible, durant une période de temps donnée avec une probabilité maximale fixée pour un produit financier ou un portefeuille. Si la "VAR à 1 jour à 90%" est pour votre portefeuille de -5%, cela signifie que vous avez moins de 10% de chance de perdre plus de 5% de sa valeur demain. 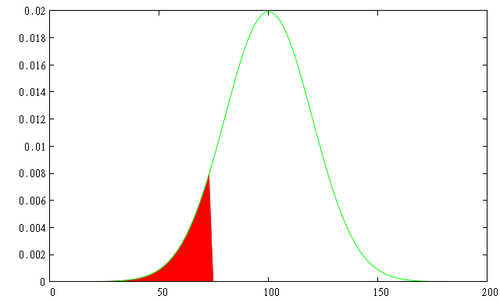Dans un langage plus mathématique, la valeur d'un produit financier ou d'un portefeuille peut être représentée par une distribution de probabilité. Le graphique ci-dessus représente une courbe de probabilité possible pour la valeur d'un produit pour le prochain jour ouvré. Le prix de clôture moyen est 100€ et l'axe vertical montre la probabilité que le prix correspondant se réalise. L'aire rouge représente une probabilité cumulée de 10%. Un prix inférieur à 75€ dans la zone rouge a donc moins de 10% de se produire. En conclusion la Value At Risk à 1 jour et à 90% est 25€=-25%. Pour un échantillon de données, cela correspond au percentile à 10%.

Pour des produits listés comme des options et des obligations, nous avons suffisamment de données historiques pour évaluer le percentile basé sur cet historique. Pour des produits plus exotiques, comme les options qui sont fabriquées à la demande, les prix ne sont pas disponibles. Dans ce cas, les prix sont simulés et le même calcul est réalisé de la même façon que pour des données historiques.

La simulation de Monte-Carlo

La méthode utilisée repose sur un algorithme basé sur un échantillon aléatoire. Cette technique est connue sous le nom de méthode de Monte-Carlo, en référence au jeu de hasard des casinos de Monte-Carlo. Pour décrire brièvement comment une telle méthode peut conduire à un résultat précis en se basant sur des nombres aléatoires, nous allons détailler comment calculer le nombre . Prenons un carré de côté 1.0 et un quart de cercle de rayon 1.0 comme sur le schéma ci-dessous. 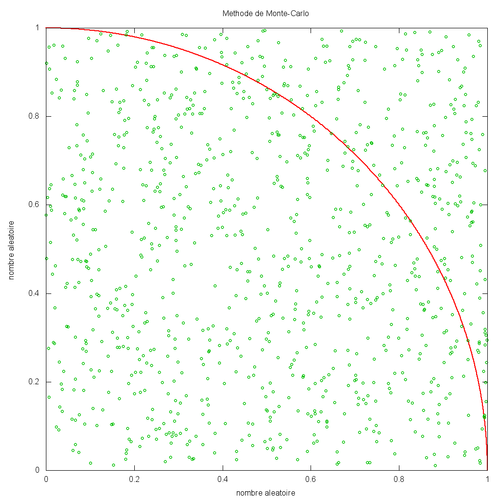Si vous générez deux nombres aléatoires indépendants x et y avec une distribution uniforme entre 0 et 1.0, cela revient à disperser aléatoirement des points sur ce carré. Avec une infinité de points, la surface sera totalement recouverte. Le rapport entre le nombre de points dans le cercle () et le nombre total de points dans le carré sera égal au rapport entre l'aire du quart de cercle et celle du carré. Soit }{1\times1}=\frac{\pi}{4}). L'algorithme consiste à générer des couples aléatoires puis à compter la proportion de tirages à l'intérieur du cercle. Multiplier le résultat par 4 nous donne une approximation du nombre .

Pour les besoins du calcul financier, nous remplacerons les points aléatoires par des simulations aléatoires des paramètres de marché (tels le prix du sous-jacent, le taux d'intérêt) et l'aire du cercle par un modèle permettant de calculer la valeur du portefeuille en fonction de ces paramètres.

Un exemple simple : un portefeuille avec un call

Pour les besoins de cet article, j'ai choisi un portefeuille extrêmement simple avec un unique produit : dans le jargon une position longue sur un call (c'est-à-dire que le propriétaire du portefeuille a acheté un call). Un call est une option d'achat, c'est-à-dire un contrat financier donnant la possibilité mais pas l'obligation au détenteur d'acheter une certaine quantité d'un instrument financier (le sous-jacent) à une date donnée (la date de maturité) et à un prix fixé (le prix d'exercice). Le vendeur reçoit en échange de ce contrat des honoraires (la prime).

Nous pouvons construire un premier modèle du bénéfice de ce call en connaissant le prix que le sous-jacent aura à maturité (disons dans un an). 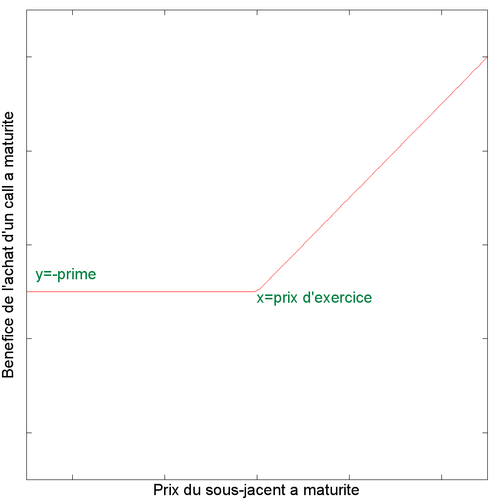Nous souhaitons désormais être capable de construire un modèle pour le prix de ce call avec une maturité de un an. Mais aujourd'hui nous ignorons le prix que ce sous-jacent pourra avoir dans un an. Je ne rentrerai pas plus dans les détails et je dirai simplement qu'il existe des modèles plus compliqués. Ils sont basés sur la théorie des probabilités : le modèle de Black and Scholes permet de déterminer le prix d'un call en connaissant uniquement :

les caractéristiques du call : la date de maturité et le prix d'exercice
le prix du sous-jacent aujourd'hui (non plus dans le futur comme dans le précédent modèle)
le taux d'intérêt sans risque
un paramètre des marchés de dérivés connu sous le nom de volatilité implicite

Le taux d'intérêt sans risque peut être estimé à partir de la valeur actuelle de l'Euribord (proche de 5%). La volatilité implicite peut être déduite d'options listées ou d'un indice spécifique tel le VIX ou le VAEX (regardez ces échantillons de prix). Dans cet exemple, nous prendrons une valeur de 20. Le modèle de Black and Scholes pour un simple call peut être exprimé par une formule un peu complexe mais fermée (c'est-à-dire qu'elle est prédictible et peut être facilement calculée). Il s'agit d'une expression arithmétique utilisant exp, sqrt et N(.) (la probabilité cumulée d'une distribution normale appelée LOI.NORMALE.STANDARD dans Excel). Regardez cet article de Wikipédia pour plus de détails et le graphique de la version anglaise montrant comment le prix de l'option varie quand le prix du sous-jacent varie.

Estimation de la puissance de calcul requise

En combinant ces deux méthodes, nous pouvons estimer la VAR de notre portefeuille exemple. Les étapes requises sont :

Générer des données pour les trois paramètres que nous avons choisis : le prix de l'option sous-jacente, le taux d'intérêt et la volatilité implicite. Pour rester simple, nous faisons l'hypothèse que ces trois paramètres suivent des distributions normales indépendantes.
Calculer pour chaque ensemble de paramètres générés le prix de l'option correspondant avec l'expression de Black and Scholes
Calculer le percentile à 1% pour la distribution des prix d'option

Ce calcul simple est relativement court mais un grand nombre d'échantillons sont requis pour obtenir une précision correcte au niveau du résultat final. Pour donner un ordre de grandeur, environ 100000 échantillons sont requis dans notre cas. En utilisant Excel 2007 sur mon portal (un Dell Latitude avec un core i7 avec 2 cores avec hyperthreading et 4 GB de RAM) 100000 échantillons ont pris approximativement 2 s. pour une option et un seul paramètre simulé (le prix du sous-jacent). Sur le même portable un programme Java mono-threadé (utilisant uniquement un core) a pris environ 160 ms. Cela semble être rapide mais dans la vraie vie chaque produit exotique d'un portefeuille est une combinaison de plusieurs options. Un portefeuille contient probablement des dizaines ou des centaines de produits exotiques. De plus, une modélisation plus complexe que le modèle de Black and Scholes est aujourd'hui utilisée nécessitant des calculs plus complexes ou plus d'échantillons. La puissance de calcul requise est au final très importante.

L'architecture de calcul en grille

De façon à gérer une telle puissance de calcul au meilleur coût, l'architecture en grille de calcul est la meilleure solution. Une grille est une architecture de calcul qui autorise à coordonner un grand nombre de ressources distribuées autour d'un objectif commun. Dans notre cas, ces ressources sont des ordinateurs dont les processeurs sont utilisés pour réaliser ce calcul. Ces ressources peuvent être distribuées, c'est-à-dire distantes physiquement et liées par un réseau informatique. 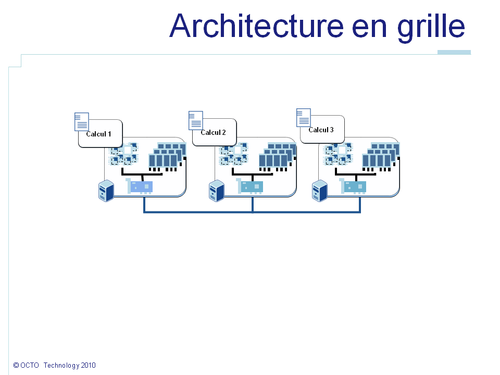Chacun de ces N noeuds (ordinateurs) effectueront une petite part du calcul sur leurs processeurs, autorisant à fournir le résultat (dans un monde idéal) N fois plus rapidement qu'avec un simple ordinateur. Nous allons décrire comment écrire l'algorithme pour cette grille.

Comment calculer la VAR

De façon à être capable de découper, de distribuer le calcul de la VAR, l'algorithme doit être adapté. La façon la plus simple d'estimer la VAR d'un portefeuille (en première approximation) serait de sommer les VAR de chaque produit. La VAR de chaque produit peut alors être calculée indépendamment sur chaque noeud. L'algorithme peut dans ce cas rester inchangé. Cependant, cela ne permet pas d'accélérer le calcul de la VAR pour notre portefeuille avec un simple call. Une raison plus générale de changer cet algorithme est qu'il ne permet pas d'augmenter le nombre d'échantillons et ainsi la précision du calcul.

Malgré ces difficultés, voyons maintenant comment nous allons l'implémenter. Nous pouvons utiliser le pattern map/reduce. Le pattern vient de la programmation fonctionnelle où la fonction map m() list applique la fonction m() à chaque élément de la liste, et reduce r() b list agrège le paramètre b et toutes les valeurs de la list dans une simple valeur. Prenons un exemple concret :

L'expression map (\x -> 2*x) [1,2,3] renvoie [1*2,2*2,3*2]=[2,4,6].
L'expression reduce (\x y -> x+y) 0 [2,4,6] renvoie 0+2+4+6=12.

Avec un tel pattern, la liste peut être subdivisée en N sous listes envoyées au N noeuds de la grille. Dans cet exemple, 1 est envoyé au premier noeud, 2 au second, etc. Le code de la fonction \x --> 2*x, envoyé en même temps que les valeurs, est exécuté sur chaque noeud : 2*1 par le premier, 2*2 par le second, etc. Vous devez imaginer que \x -> 2*x est remplacé par une fonction nécessitant beaucoup de puissance de calcul. L'exécuter de façon parallélisée permettra donc de diviser le temps de calcul requis. Tous les résultats 2, 4, etc. sont renvoyés aux noeuds à l'origine de la demande. Les résultats sont concaténés en une liste [2,4,6] et la méthode reduce (\x y -> x+y) est appliquée. La fonction map est répartie sur les différents noeuds mais pas la fonction reduce qui est exécutée sur le noeud à l'origine de la demande.

Dans notre exemple, chaque génération d'échantillons sera représentée par un élément de la list. La méthode map() générera sur chaque noeud les données exemples, calculera le prix du call correspondant et retournera le résultat. Ensuite tous les prix seront envoyés au noeud exécutant la méthode reduce(). La méthode reduce() calcule le percentile à 1% de ces données. Et de cette façon cela nous donnera la VAR à 99% du portefeuille.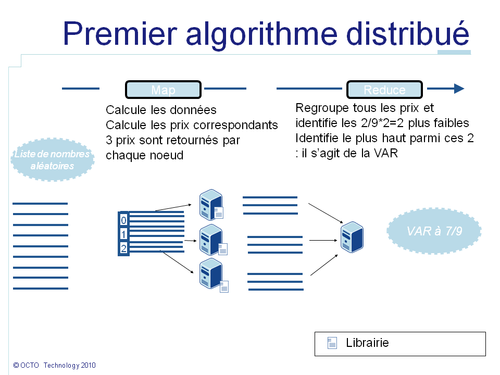

Cette première version fonctionne, mais peut encore être améliorée un peu.

Tout d'abord, la fonction reduce() n'est pas distribuée, il est donc préférable de minimiser la quantité de données qu'elle doit traiter
Ensuite, transférer 100000 prix à travers le réseau est consommateur de ressources. En pratique, la bande passante est une ressource critique dans une grille

En investiguant un peu plus, on peut noter que calculer le percentile à 1% revient à trier les données puis à prendre la valeur la plus haute parmi le 1% de valeurs les plus faibles. Je fais l'hypothèse que pour le cas métier imaginé pour cet exemple les résultats intermédiaires peuvent être ignorés. Dans ce cas, cet algorithme peut également être distribué. L'idée est que les 10 valeurs les plus faibles d'un ensemble sont contenues dans l'ensemble de 10 valeurs les plus faibles de chacun de ces sous-ensembles. Imaginons que je recherche les 4 cartes les plus fortes d'un jeu de cartes de poker. Le pack a été divisé par couleur en 4 tas. Je peux rechercher dans chaque tas les 4 cartes les plus fortes. J'obtiendrai un as, un roi, une dame et un valet et ce pour chaque couleur. Ensuite, je peux regrouper ces 4*4=16 cartes et chercher de nouveau les 4 cartes les plus fortes. J'obtiendrai les 4 as. Ce raisonnement peut être généralisé quelque soit le partitionnement du paquet et quelque soit le nombre de partitions.

Imaginons que dans notre cas nous souhaitions calculer 100000 échantillons sur 2 noeuds. Le percentile à 1% correspond à la valeur la plus haute parmi les 1000 valeurs les plus faibles. Sur chaque noeud, 50000 valeurs ont été calculées. Sur chaque noeud nous pouvons prendre les 1000 valeurs les plus faibles et les envoyer comme résultat à la place des 50000. De cette façon la fonction reduce() assemblera seulement 2 listes de 1000 valeurs, isolera les 1000 valeurs le plus faibles et identifiera la plus haute. En effet, même dans le pire des cas où les 1000 valeurs les plus faibles auraient toutes été générées sur un même noeud, celui-ci fournira ces 1000 valeurs, garantissant que le percentile sera toujours transmis. Une telle optimisation permet de réduire par 50 la quantité de données transmises à travers le réseau. Le bénéfice décroit lorsque le nombre de noeuds augmente. Dans le pire des scénarios avec 100 noeuds il n'y a plus de bénéfice. Mais en pratique, distribuer de petites listes d'échantillons est contre-productif car le surcoût de distribution est plus important que le gain possible. Ainsi, une telle optimisation permet de minimiser les ressources requises.

L'algorithme final est résumé dans le schéma ci-dessous :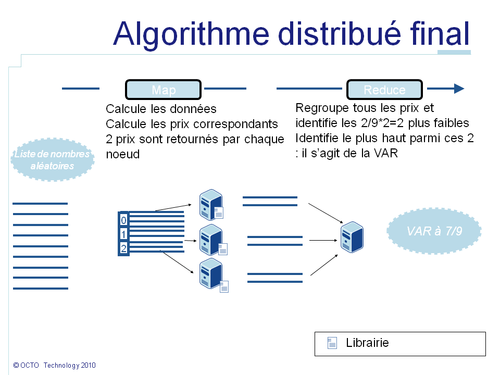

Conclusion

D'un point de vue métier, l'estimation des risques est devenue de plus en plus importante pour les institutions financières afin de prévenir les pertes sur des marchés fluctuants. De plus, les nouvelles normes de régulation telles Bâle III et Solvabilité (Solvency) II prennent en compte la VAR dans leurs exigences. L'efficacité des calculs de ces valeurs est un pré requis forme pour le système d'information des institutions financières. A travers un exemple très simple, cet article a montré que ces calculs reposent sur la génération de données aléatoires et la réalisation de calculs mathématiques pour évaluer la valeur du portefeuille pour chaque échantillon. Le nombre d'échantillons requis et parfois la complexité dans la méthode de calcule nécessitent des architectures spécifiques pour terminer ces calculs dans des temps raisonnables. La grille de calcul est l'architecture la plus à jour pour répondre à ce genre de problématique. Le pattern map reduce est l'une des façons les plus simples d'écrire un algorithme qui bénéficie de l'accélération rendue possible par le calcul en grille. La compréhension des besoins métiers est un point important pour optimiser le code. Dans cet exemple, ignorer les résultats intermédiaires permet d'accélérer le calcul. Dans un autre article, je décrirai une implémentation de cet exemple en utilisant un intergiciel (middleware) de grille de calcul et je donnerai quelques chiffres de performance.