Green AI - les algorithmes en question

Les auteurs tiennent à remercier chaleureusement Benjamin Scellier, coauteur avec Yoshua Bengio de Equilibrium Propagation pour son temps, sa disponibilité et sa relecture attentive et bienveillante.

Si on parle de sauvegarde de notre planète à un Data Scientist, il est probable qu’il s’imagine tout de suite utiliser son savoir pour développer des algorithmes capables d’optimiser l’utilisation de nos ressources ou bien de régler une bonne fois pour toute le problème du réchauffement climatique en le prenant pour ce qu’il est, un problème scientifique qu’il faut donc résoudre par la science.

Même si la Data Science a très probablement son rôle à jouer sur ce point, cet article n’est pas là pour cela. Il s’adresse au Data Scientist pour ce qu’il est aujourd’hui : un pollueur comme un autre.

Cet article ne se veut pas non plus militant ou dénonciateur d’une profession. D’ailleurs, il est écrit par 2 Data Scientists qui ont participé à pas mal de Kaggle et autres compétitions de Data Science et qui ont donc quelques tonnes de CO₂ de dettes accumulées ces dernières années vis-à-vis de la planète, qui feront toujours de la Data Science avec disons, un regard un peu différent sur la matière qu’ils manipulent.

Mais avant de partager ces nouvelles connaissances, rappelons peut-être quelques fondamentaux sur le principal outil du Data Scientist : le machine learning.

Back to basics : la performance algorithmique du machine learning

Il a fallu attendre 1998 pour voir la France gagner la coupe du monde et disposer d’une définition formelle du Machine Learning. On la doit à Tom Mitchell qui définit le machine learning comme étant la famille d'algorithmes qui permettent aux programmes de s’améliorer par expérience,  cette amélioration étant quantifiable par une mesure de performance.

On y apprend une chose simple : plus on a de données (l’expérience), plus la performance à accomplir une certaine tâche augmente.

Entre-temps, le Big Data étant passé par là et réglant à peu près la question du volume de données, peut-être Tom Mitchell avait-t-il involontairement contribué à lancer toute une génération de Data Scientist dans une course sans limite : celle de la recherche de performance.

En tant que Data Scientist, travailler sur une science quantifiable est une chance incroyable. En effet, nous savons créer une boucle de feedback avec une mesure très concrète de l’apport d’une idée donnée en termes de performance. Avec peut-être cette petite musique de fond qui laisse à penser qu’on mesurerait par là-même les compétences du Data Scientist...

Les plateformes de compétitions de Data Science (Kaggle notamment) se sont d’ailleurs vite popularisées grâce à ce lien très fort qui existe entre performance algorithmique pure et la compétence du Data Scientist.
Alors, être un bon Data Scientist, c’est être celui qui a la meilleure performance sur un problème donné ?

On aime, chez OCTO, à ne plus penser cela. Et plusieurs gardes-fous ont émergé ces dernières années renforçant cette posture :

L'industrialisation du code. La recherche absolue de performance mène souvent à produire des modèles très complexes (apprentissage à plusieurs étages, combinaison de modèles, etc.) qui, bien que très performants, sacrifient complètement les capacités d’industrialisation d’un tel modèle. Le concours organisé par Netflix en 2009 attribuant 1M$ à l’algorithme qui améliore son score de recommandation en est l'illustration. Le modèle gagnant fut impossible à déployer  en production car trop complexe.^[1]

L’explicabilité. La généralisation des modèles non-linéaires en machine learning a fait frémir plus d’un statisticien, habitué de leur côté à réaliser des modèles linéaires dotés d’une bonne dose d’explicabilité (mais moins performants). Et savoir expliquer un modèle prédictif, c’est plutôt rassurant. En effet, faire confiance à une machine pour réaliser des tâches cognitives a déjà un côté effrayant en soi. On ne peut pas en plus confier ces tâches à d’absolues boîtes noires.  Ainsi, sauf dans des cas très spécifiques, on verra de moins en moins de Data Scientists sacrifier toute explicabilité au profit des quelques millionièmes de performance complémentaire (dont l’apport concret est souvent discutable, si ce n’est pour l’ego du Data Scientist). Et on voit une course croissante vers l’explicabilité des prédictions, y compris lorsqu’elles sont issues de modèles fortement non-linéaires ou de réseaux neuronaux. Même s’il reste encore beaucoup de travail à accomplir pour trouver le compromis entre performance et l’explicabilité, disons que le Data Scientist est plutôt en bonne voie.

On pourrait citer enfin l’utilisabilité qui rappelle, si besoin était, qu’il y a un utilisateur au bout du modèle de Data Science. Il a ses contraintes et ses besoins qui peuvent là-encore constituer un garde-fou très efficace à la performance pure.

Si la recherche frénétique de performance est l’ennemie de l’industrialisation, de l’explicabilité ou encore de l’utilisabilité, elle est aussi l’ennemie de notre planète.

Comme tout bilan énergétique, il est très difficile d’établir celui d’un modèle de machine learning en production mais nous pouvons essayer de passer en revue les différentes étapes entre la première idée (et l’étape de cadrage) et son implémentation en production pour au moins identifier les grands “postes de dépenses énergétiques” et donc les principaux leviers.

Nous avons choisi d’étudier les 3 suivants :

• Le levier code. Autrement dit, la façon dont les algorithmes sont implémentés.
• Le levier hardware. Autrement dit, le matériel sur lequel ce code est exécuté.
• Le levier méthodologique. Autrement dit, l’ensemble des choix que fait un Data Scientist dans son processus de développement.

Le sujet étant aussi vaste que passionnant, nous vous présentons dans ce premier article d'une série de 3 ce que nous avons appris sur le premier levier.

Levier 1 - Le code

Les algorithmes de Machine Learning que nous utilisons ont tous à peu près la même genèse : un chercheur ou un groupe de chercheurs publient un papier présentant leur apport à l’état de l’art avec comme souvent un dernier chapitre qui présente l’évaluation de cette approche par rapport à l’état de l’art. Et devinez la grandeur sur laquelle cet apport est mesuré ? Bingo, la performance !

Le grand Leo Breiman lui-même, présentait l’apport du Random Forest dans le papier éponyme (2001) en termes de gain de performance par rapport à une star algorithmique de l’époque, adaboost, sur différents datasets. Une pratique élevée au rang de standard.

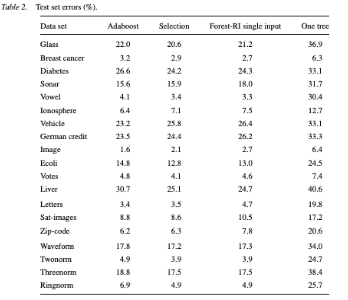
L. Breiman - random forests vs adaboost (2001)

Pour ce qui est du deep learning, disons qu’il est difficile de trouver un papier présentant une nouvelle idée sans le petit tableau de gain de performance la “validant” ainsi.

Ce n’est pas une ineptie en soi, il est indispensable de pouvoir comparer les algorithmes entre eux et, après tout, c’est bien ce qu’on lui demande au machine learning, d’être toujours plus performant !

Certes, mais à quel prix?

Rares sont les papiers qui s'intéressent au coût de ce gain de performance. D’ailleurs, sur quel axe mesurer ce coût : l’argent, le temps, la puissance machine ou même l’empreinte carbone ? En Juillet 2019, Schwartz et al. introduisent dans leur bien-nommé papier “Green AI” cette notion de coût d’une AI.

L’article suggère que le coût d’une AI croit linéairement avec ces 3 grandeurs :

• Le coût de processing d’une seule observation ou exemple (E)

• La taille du dataset (D)

• Le nombre d’expérimentations, notamment pour optimiser les hyperparamètres du modèle (H)

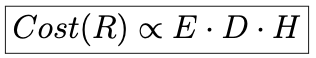
Une proposition de coût du machine learning (schwartz et al.)

De l’aveu même des auteurs, cette formulation a ses limites (non prise en compte du nombre d’epochs notamment) mais elle est simple à comprendre et nous permet de nous concentrer, pour notre premier levier, sur le coût de processing d’une seule observation. En effet, on peut considérer que la taille du dataset ne varie pas et que le nombre d’expérimentations fait partie des choix que fait le Data Scientist et sera donc traité dans le levier méthodologique.

L’introduction de ce “coût” permet d’apporter une dimension supplémentaire pour l’appréciation d’un nouvel algorithme ou d’une nouvelle architecture de réseau de neurones.

On se rendrait peut-être compte qu’on s’extasie parfois devant un nouvel algorithme qui améliore les performances certes, mais de façon ridicule par rapport au surcoût engendré. On pourrait alors combiner coût et gain de performance dans ce qu’on pourrait qualifier de ROI algorithmique, qualifier le travail de recherche et l’apprentissage comme un investissement dont on mesurerait le retour comme pour n’importe quel investissement.

Ceci étant dit, comment caractériser concrètement ce coût de processing pour lui donner un caractère reproductible et indépendant d’autres paramètres (comme le hardware) ?

Les auteurs du même article suggèrent assez naturellement d’utiliser le FLOP, ou nombre d’opérations flottantes. Pour faire simple, il s’agit de compter toutes les opérations mathématiques de base, qu’on peut restreindre à l’addition et la multiplication^[2], entre 2 nombres flottants.

Même s’il serait intéressant de lever le capot du Random Forest ou du Gradient Boosting, il y a fort à parier que les stars de la consommation énergétique se trouvent du côté des réseaux neuronaux lors de la phase d’apprentissage.

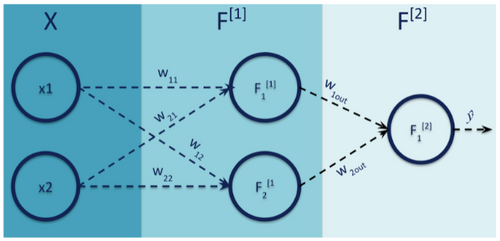
Dans un réseau de neurones en cours d’apprentissage, le processing d’un seul exemple correspond à un feed-forward, qui permet d’avoir une première estimation par notre réseau de neurones et à une back-propagation, opération qui vise à modifier les poids en fonction de leur contribution propre à l’erreur. Voyons cela schématiquement :

Un réseau de neurones dans son plus simple appareil

Pour un exemple d’apprentissage x et avec les notations de notre schéma, on peut voir la sortie de notre réseau de neurones (de la phase de feed-forward donc) comme une simple composition de fonctions et quelques FLOPs à la clé.

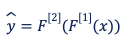
La suite des opérations est très classique : caractériser l’erreur entre notre estimation ŷ et y et propager cette erreur en suivant la règle de dérivation des fonctions composées (chain rule). Observons comment cela se passe juste pour calculer la contribution à l’erreur de w~<em>1out</em> ~ :

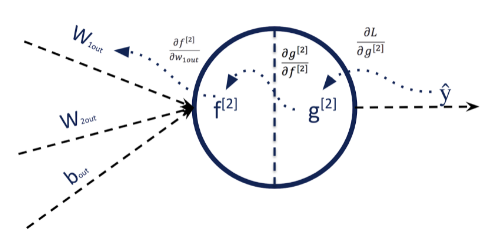
Une back-propagation en pleine action

Toutes les dérivées partielles (qui représentent les contributions à l’erreur de poids donnés) étant connues, on sait comment modifier w_{<em>1out</em>} pour améliorer la prédiction de notre réseau de neurones et plus généralement, tous les poids du réseau. Pour la back-propagation, cette opération est faite dans un batch pour tous les poids du réseau en même temps, avec son lot de FLOPs supplémentaires, outre le fait qu’on met parfois à jour seulement de façon infinitésimale les poids...

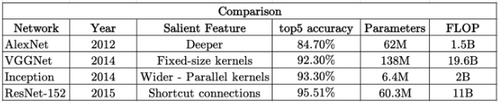
Comptez une bonne centaine de FLOP pour notre minuscule réseau de neurones avec moins de 10 paramètres pour traiter ainsi un seul exemple d’apprentissage avec seulement 2 features.Quand on sait que certains réseaux profonds ont des centaines de millions de paramètres à optimiser, le nombre d’opérations à effectuer pour réaliser un mini-batch d’apprentissage est immense en dépassant par exemple 19 milliards de FLOP avec un simple VGG de 2014.

Nombre de paramètres et FLOP de certains “vieux” réseaux de neurones

Fort heureusement, la back-propagation est un algorithme largement optimisé pour le calcul matriciel et l’avènement de GPU sans cesse plus performants ont rendu assez indolore cette étape. Mais uniquement pour le temps du Data Scientist, pas pour la planète. Et c’est sans compter les autres problèmes numériques à résoudre pour la back-propagation comme la disparition ou l’explosion de gradient^[3] qui rendent très lente voire impossible la convergence vers les poids optimaux. Et ce sont ainsi des milliards de FLOP qui auront été “consommés” pour rien.

Pour toutes ces raisons, la façon dont nous entraînons nos réseaux de neurones aujourd’hui est loin d’être bonne pour la planète.

Et pour cause, l'algorithme de back-propagation des réseaux neuronaux est considéré comme biologiquement peu plausible.

Les comparaisons machine learning et biologie sont souvent sujettes à caution, mais après tout pourquoi pas ? On demande précisément à nos réseaux de neurones artificiels de voir, de lire, d’écrire, de traduire, de conduire une voiture, autant de tâches qui jusqu’alors était la chasse gardée du vrai réseau neuronal.

Et les découvertes dans le domaine des neurosciences ont bien souvent inspiré les chercheurs en ML : les expériences de Hubel et Wiessel sur le cortex visuel du chat ont inspirés le neocognitron de Fukushima, l’action de la dopamine et le reward utilisé en apprentissage par renforcement ou encore le Relu, fonction d’activation des neurones artificiels plus proche visiblement de la façon dont nos neurones s’activent^[4].

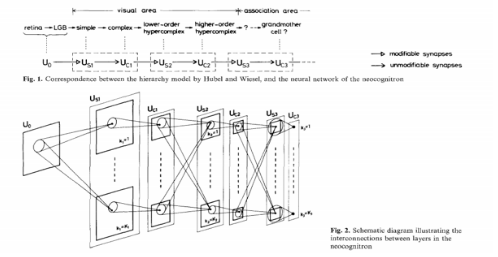
Le néocognitron de Fukushima,  ancêtre du CNN, fait directement référence aux travaux de Hubel et Wiessel sur le cortex visuel du chat

Même si, pour une tâche donnée et bien déterminée, les résultats sont comparables entre un cerveau biologique et son homologue artificiel, c’est bien dans la façon d’établir ce résultat que des différences majeures apparaissent.

Alors que l’efficacité et la faible consommation énergétique règnent en maître dans notre cerveau, le hasard^[5] et les artefacts numériques ont colonisé les réseaux de neurones artificiels.

Arrêtons-nous juste une minute sur les capacités de notre cerveau à voir.

Qui pourrait décrire la façon dont il a appris à percevoir son environnement ? Il est sans doute plus simple de décrire ce que votre cerveau n’a pas fait : passer en revue des millions d’images avec pour chacune d’elle la réponse explicite de ce qu’elle contient.

Comment vous n’avez pas appris à voir

C’est ce constat imparable qui questionne en particulier Geoffrey Hinton, pourtant un des pères fondateurs de la back-propagation. Selon lui, notre cerveau utilise un processus pas encore complètement connu mais certainement pas la back-propagation^[6].

Le problème de la cible évoqué plus haut est sans doute le plus évident pour marquer la différence entre la back-propagation et la façon dont notre cerveau fonctionne mais il en existe d’autres plus subtils qu’il convient toutefois d’avoir en tête. En plus de celui de la cible, Yoshua Bengio énumère 5 autres problèmes :

• The linear feedback problem : la phase de back-propagation est purement linéaire (contrairement à la phase de feed-forward). On ne retrouve pas cette "dissymétrie de linéarité” dans le cerveau qui fonctionne avec des neurones biologiques non linéaires.
• The weight transport problem : le même poids est utilisé dans un réseau de neurones pour la phase d’inférence et la back-propagation. Les synapses sont unidirectionnelles.
• The derivative transport problem : l’apprentissage à base de back-propagation repose sur la capacité à calculer les dérivés de chaque neurone et à l’utiliser ensuite dans la phase de back-propagation à proprement parler. Dans le cerveau, il n’est pas du tout clair comment on obtient l’équivalent de cette dérivée (ou du moins la contribution du neurone à une erreur globale) et surtout comment celle-ci serait utilisée pour apprendre.
• The spiking problem : l’activation d’un neurone artificiel est une valeur continue alors que les neurones biologiques s’activent plutôt sous forme d’impulsion binaire.
• The timing problem : les 2 phases de feed-forward et de back-propagation sont fortement intriquées temporellement, la seconde ayant besoin du résultat de la première. De plus, la mise à jour des poids s’effectue instantanément. Ces mécaniques sont incompatibles avec les délais observés dans le cerveau humain.

Il est assez logique de penser que toutes ces différences ont largement contribué à creuser le fossé immense qui sépare nos réseaux de neurones artificiels et biologiques en termes d’efficacité énergétique. Même s’il s’agit encore à ce stade d’une hypothèse, nous pouvons parier sur le fait que pour rendre le deep learning plus propre, une piste très sérieuse à explorer serait de rendre nos neurones artificiels moins...artificiels !

Il est intéressant de constater que parmi les motivations des chercheurs sur les neurones à impulsions, souvent présentés comme étant la troisième génération de réseaux neuronaux^[7], on cite généralement la possibilité de créer un modèle numérique plus proche du modèle biologique précisément pour réduire la consommation énergétique.

Peut-être le signe d’une révolution à venir, le neurone artificiel à impulsion est plutôt le domaine de recherche des acteurs hardware...nous en reparlerons dans un prochain article.

Alors faut-il attendre la troisième génération de réseau de neurones et ses dérivées ou existe-t-il en 2021 des alternatives à la back-propagation ? Oui et beaucoup (ce qui est plutôt rassurant) !

Pour certaines d'entre elles, la motivation d’être biologiquement plus plausible est une motivation clairement avérée de la recherche.

Citons par exemple Target Propagation, Equilibrium Propagation, Synthetics gradient, The HSIC Bottleneck, etc. Passons-en rapidement quelques-unes en revue.

Target Propagation

Proposé initialement par Yann LeCun dans les années 80, l’idée a été popularisée par Bengio et ses doctorants en 2014/2015. La motivation de cette approche est précisément de corriger certains défauts de la back-propagation, notamment le fait qu’elle soit non plausible biologiquement parlant comme évoqué plus haut. En particulier, l’approche proposée permettrait, d’après les auteurs, d’adresser les problèmes 1 à 4 cités plus haut (linear, weight transport, derivative transport et spiking). ^[8]

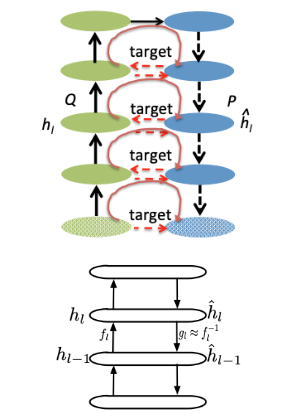
De façon très schématique, on réalise 2 feed-forward, une en avant et une en arrière.

Pour une entrée x et une sortie y, le premier modèle apprend h tel que y=h(x) et le second modèle apprend g tel que x=g(y). h et g forment ainsi un autoencoder, h étant l’encodeur dont le rôle est de créer des représentations latentes et de prédire y sachant x, et g le décodeur, dont le rôle est de générer une entrée en utilisant la sortie et les variables latentes.

Ces autoencodeurs jouent un rôle essentiel dans ce que les auteurs appellent la cible et qui est propre à chaque couche. Pour la couche i du réseau, on voudrait pouvoir ajuster localement les poids de telle sorte que globalement, le coût diminue. On apprend  pour ce faire, pour chaque couche i une cible ĥ__i_ telle que L(h(ĥ_i), y) < L(h(h_i), y_)_. Si cela est vrai, il suffit de changer les poids localement, de la couche i en utilisant par exemple cette fonction coût locale L_i=||ĥ_i-h_i__||.

Synthetic Gradients

On doit cette approche à DeepMind qui a publié en 2017 ​​Decoupled Neural Interfaces using Synthetic Gradients. Ils font remarquer que pendant la back-propagation, toutes les couches du réseau sont verrouillées, en ce sens qu’ils doivent attendre que le reste du réseau s’exécute vers l’avant et propager l’erreur vers l’arrière avant d’être mise à jour. C’est cette contrainte qu’ils essaient de lever en découplant l’acquisition de l’erreur globale et la mise à jour des poids. Assez naturellement, cette approche adresse le problème 5 (timing problem) cité plus haut.

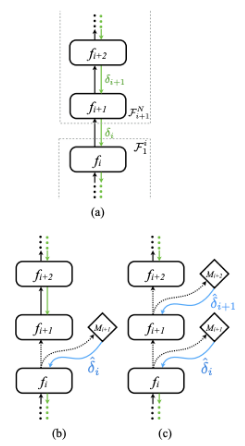
Les auteurs suggèrent de créer des modèles permettant d’estimer le gradient à chaque couche, qu’on peut qualifier de gradient synthétique. C’est ce gradient synthétique, disponible sans attendre la back-propagation qui est utilisé pour mettre à jour localement les poids.

L’apport est très intéressant : on peut découpler les graphes de calculs, les mettre à jour indépendamment et de façon asynchrone !

Dans le schéma ci-contre, la figure (a) représente une section F₁^N d’un réseau de neurones classique.

L’introduction d’un gradient synthétique (b) à la couche i coupe le réseau en 2 sous-réseaux F₁ⁱ et F_i+1^N qui peuvent être mis à jour indépendamment.

Introduire un gradient synthétique à chaque couche (c) découple le réseau en N couches indépendantes.

Equilibrium Propagation

Alors que les approches citées précédemment explorent la voie du biologiquement plausible, Equilibrium Propagation explore celle du physiquement plausible, autrement dit les lois et les équilibres naturels que nous trouvons dans la physique.

C’est en 2016 que Yoshua Bengio et Benjamin Scellier évoquent l’Equilibrium Propagation - EqProp - comme une alternative moins énergivore à la back-propagation dans l’article "Equilibrium Propagation: Bridging the Gap Between Energy-Based Models and back-propagation".

Cette approche s'inscrit dans une démarche globale visant une plus grande frugalité du ML appelée “energy-based models”. L’idée étant de réaliser les calculs dans des “substrats physiques” qui font meilleur usage des lois de la physique.

Un levier efficace pour réduire l'écart abyssal de consommation énergétique entre le cerveau et les algorithmes ML s’exécutant sur des microprocesseurs est de s’appuyer, à l’image des synapses du cerveau, sur des informations disponibles localement.

S’appuyant sur de solides garanties théoriques, l’EqProp fonctionne en 2 phases, au cours desquelles le système physique évolue d’abord librement vers un état d’équilibre, minimisant son énergie. Puis par “poussée” vers la cible en mettant localement à jour les poids du réseau en fonction des seuls états des neurones directement connectés jusqu’à atteindre un nouvel état d'équilibre. Les auteurs ont mathématiquement démontré que les mises à jour des poids avec l’EqProp suivent exactement le gradient d’une fonction d'objectif lorsque la poussée est effectuée avec une force infinitésimale.

Bien que cet algorithme calcule le gradient d'une fonction d’objectif, tout comme la back-propagation, il ne requiert pas de calcul spécifique pour la deuxième phase. Le processus itératif alterne apprentissage vers l’avant pour l’inférence et calcule d’erreur de manière prospective. Tout comme notre cerveau avec sa propre biophysique.

Avec du recul, Benjamin nous a partagé son point de vue sur son article co-écrit avec Yoshua Bengio sur EqProp : “D’un côté je suis fier de cet article pour la formule du calcul du gradient que l'on établit. D’un autre côté je pense qu'on a un peu trop insisté sur le côté “biologiquement plausible” de EqProp et pas assez sur les implications physiques. Si on prend au sérieux l'idée d’utiliser l'énergie d’un vrai système physique comme fonction d'énergie, EqProp ouvre la voie pour construire des machines qui utilisent directement les lois de la physique pour faire les calculs à l'inférence et pendant l'entraînement. A mon avis, c'est ça la contribution la plus importante de EqProp. Notre théorème et notre algorithme s’adressent avant tout à la communauté des physiciens, et de façon secondaire à celle des chercheurs en neuroscience. “

Même si en pratique les auteurs reconnaissent que l'implémentation de l’EqProp standard ne s'adapte pas aux tâches visuelles plus difficiles que MNIST, il y a fort à parier que c’est là le début d’une approche en devenir basée sur des concepts élégants offrants de nombreux avantages potentiels pour l'apprentissage efficient de réseaux très complexes.

Il faudra toutefois attendre avant que ces gains d'efficacité ne soient pleinement réalisés dans une perspective neuromorphique avec une "puce de rêve" qui utiliserait les mêmes circuits pour l'inférence et le calcul de gradient. Mais nous aurons l’occasion de vous en parler plus longuement lorsque nous évoquerons le levier hardware dans la seconde partie de cette série.

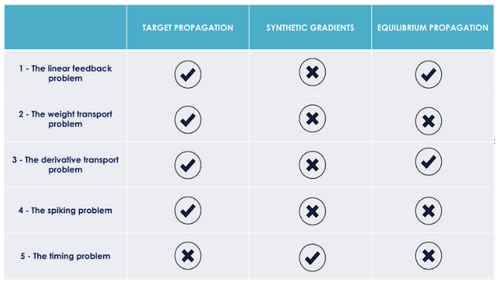
A date, ces 3 alternatives à la back-propagation adressent partiellement, en plus du problème de la cible, les 5 problèmes évoqués par Yoshua Bengio comme l'illustre le tableau de synthèse ci-dessous.

Les problèmes adressés par quelques alternatives à la back-propagation

Néanmoins, il est heureux de constater qu’un vaste champ de recherche s’est ouvert depuis quelques temps sur le développement d’un algorithme d’apprentissage des réseaux neuronaux qui soit plus biologiquement plausible. Donc moins énergivore. Donc, plus respectueux de notre planète.

Seulement voilà, la back-propagation est si largement répandue, si simple à comprendre et quand même diablement efficace derrière son armée de GPU. Il y a encore du travail pour qu’un algorithme la supplante, ce qui laisse entrevoir de futures recherches mêlant neuroscience (et science physique) et machine learning absolument passionnantes !

Gageons qu’un tel algorithme devra satisfaire au moins les conditions suivantes :

• Avoir des performances équivalentes en terme de résultat.
• Combattre les artefacts numériques (comme la disparition/explosion de gradient) pour ce qu’ils sont : du pur gâchis.
• Être BEAUCOUP plus efficient et BEAUCOUP plus respectueux pour la planète.

Bien entendu, ces nouveaux algorithmes devront aussi être cohérents avec les autres enjeux cités en introduction, notamment l’interprétatabilité.

Nous avons passé en revue quelques raisons qui rendent un algorithme (parmi d’autres) comme la back-propagation en l’état tout simplement incompatible avec le défi du dérèglement climatique. En particulier, le premier levier du code nous a permis d’explorer les défis qui restent à résoudre pour rendre l'entraînement des réseaux neuronaux plus plausibles biologiquement.

Dans un prochain article, nous verrons pourquoi nos algorithmes de machine learning mettent à mal le hardware sur lequel ils sont exécutés.

[1]  https://netflixtechblog.com/netflix-recommendations-beyond-the-5-stars-part-1-55838468f429

[2]  Soustraire revient à ajouter un nombre négatif et diviser à multiplier par un inverse

[3]  Lorsque les gradients se rapprochent de 0 pour les couches inférieures, ces dernières sont entraînées très lentement, voire pas du tout. A l’inverse, si les poids sont très importants, les gradients de ces couches, impliquant le produit de nombreux de nombreux termes de grande taille, deviennent trop grands pour qu’il y ait convergence

[4]  Deep learning improved by biological activation functions https://arxiv.org/pdf/1804.11237.pdf

[5]  Pensez à l'initialisation des poids, au dropout, au tirage aléatoire du mini-batch pour la SGD, etc.

[6]  Assessing the scalability of biologically-motivated deep learning algorithms and architectures https://arxiv.org/pdf/1807.04587.pdf

[7]  La première étant le perceptron et ses dérivés, la deuxième génération, le deep learning que nous connaissons actuellement

[8] How Auto-Encoders Could Provide Credit Assignment in Deep Networks via Target Propagation https://arxiv.org/abs/1407.7906