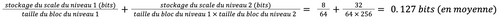Fine-Tuning d’un LLM avec la méthode PEFT : Théorie

le 07/04/2025 par Jean-louis Debezia
Tags: Data & AI, Intelligence Artificielle, Data Science, Machine Learning, Deep Learning

Introduction

Tout d’abord avant de commencer cet article, je tiens à remercier toutes les personnes qui m’ont aidé à rédiger cet article, merci à DORB, STIL, TEIM, ISDE, PESO, GIRE, PPR, MOAL, BACO.

Avec l'essor des LLMs, leur adaptabilité à des tâches spécifiques est devenue un enjeu majeur pour la recherche et l’industrie. Cependant, les besoins de personnalisation pour des cas d'utilisation spécifiques sur des domaines particuliers nécessitent des solutions plus efficaces et moins coûteuses que l'entraînement complet d'un modèle. C'est dans ce contexte que la méthode de Parameter Efficient Fine-Tuning (PEFT) trouve toute sa pertinence. Cette approche permet d'optimiser la performance des modèles préexistants en ajustant uniquement une petite fraction de leurs paramètres. Dans cet article, nous parlerons d’abord des différentes méthodes utilisées pour améliorer les performances d’un LLM à la réalisation d’une action. Ensuite, nous verrons dans quel cas il peut être intéressant de fine-tune un LLM et étudierons la méthode PEFT avec ses différents algorithmes et stratégies d’optimisation des calculs.

Méthodes d'amélioration des performances d’un LLM

Les modèles de fondation, tels que GPT-3 ou BERT, sont entraînés sur de vastes corpus de données textuelles générales, ce qui leur permet d'acquérir une compréhension étendue du langage naturel. Cependant, lorsqu'il s'agit de tâches spécifiques, ces modèles peuvent ne pas être suffisamment performants sans ajustements. Pour rappel, voilà la définition proposée par la CNIL sur les modèles de fondation

“Il s’agit d’une catégorie de modèles d’IA entraînés sur un ensemble de données dont la quantité et la diversité sont particulièrement importantes, dont les capacités sont générales et qui peut être adapté à une grande diversité de tâches distinctes.”

CNIL (Commission Nationale de l’Informatique et des Libertés)

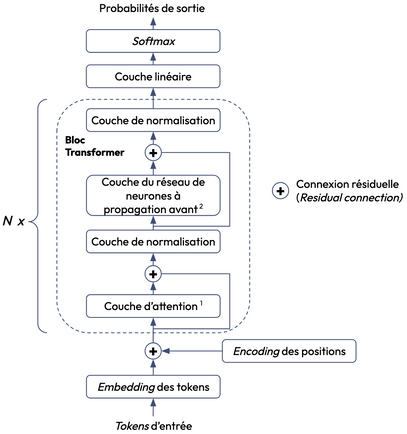
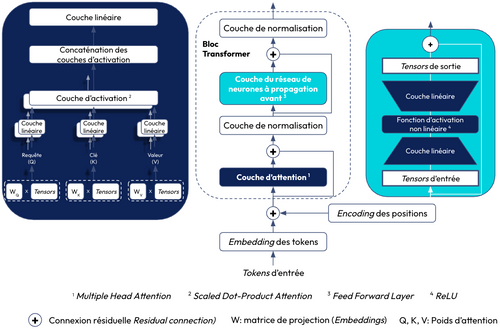
Les Large Language Models (LLMs) sont un type de modèle de fondation. Ils se basent sur l'architecture des Transformers Decoder-only qui est utilisée pour les tâches de génération (cf. figure 1). Si vous souhaitez approfondir le sujet, je vous conseille ce papier de recherche qui présente le développement des modèles de fondation et leurs capacités de raisonnement en faisant une analogie avec le cerveau humain.

Représentation de l’architecture des Transformers Decoder-onlyFigure 1: Représentation de l’architecture des Transformers Decoder-only (GPT, LLaMA, Falcon)

Dans cet article, nous parlons uniquement des LLMs instructed, c’est-à-dire qu’ils ont été fine-tuned pour comprendre et suivre des instructions en langage naturel (par exemple résumé/traduction/synthèse de texte). Donc contrairement aux LLMs de base (non instructed), il ne s’agit pas juste de prédire le token suivant mais de répondre à une consigne explicite, comme le ferait un assistant. Ce sont très souvent ces modèles qui sont utilisés pour le développement d’applications à base de LLMs. La principale raison est son alignement comportemental. Le LLM instructed suit mieux ce qu’on attend de lui (moins de confabulations, pas de réponse toxique). Il comprend des consignes claires et répond de façon structurée, ce qui permet une meilleure interaction avec l’utilisateur. Si vous souhaitez creuser le sujet des LLMs instructed, je vous recommande ce papier de recherche.

Pour améliorer les performances de ces LLMs sur des cas d’usage spécifiques, plusieurs approches ont été développées :

  • Prompt Engineering : Donner des prompts structurés (instruction, contexte, format réponse souhaité) au LLM afin de maximiser les performances du modèle pour des tâches spécifiques sans changer l’architecture du LLM. Pour cela, il existe 2 approches:
    • Zero-shot learning : Décrire une tâche au LLM sans lui donner un exemple et sans être forcément préalablement être entraîné dessus
    • Few-shot learning : Décrire une tâche en donnant des exemples de réponses attendues (permettant au LLM de comprendre le problème)
  • Chain-of-Thought (CoT alias Chaîne de pensée) : Générer un mécanisme de la pensée sous la forme d’une succession d'étapes de raisonnement, écrites en langage naturel qui conduit à la réponse finale. En étant guidé par des exemples, le modèle est incité à suivre un schéma de raisonnement lorsqu'il répond à la question.
  • Retrieval-Augmented Generation (RAG): Créer un moteur de recherche dans une base de données externe (base documents/corpus de texte) pour récupérer les passages ou documents pertinents par rapport à la tâche à réaliser afin d’obtenir des réponses plus précises et contextuelles et les intégrer au prompt avant la génération de la réponse (Combinaison connaissance du LLM pré-entraîné et la capacité de recherche d’informations)
  • Reinforcement Learning from Human Feedback (RLHF alias Apprentissage par Renforcement à partir de retours d’humains) : Collecter des évaluations de l'utilisateur sur les réponses du LLM afin de les utiliser comme récompense pour le modèle d’apprentissage par renforcement dans le but d'ajuster les paramètres pour améliorer les réponses

Parmi ces approches, on retrouve uniquement de l’adaptation à une tâche spécifique, mais comment faire si l’on souhaite que le LLM apprenne sur un domaine spécifique ? C’est justement là qu’intervient le fine-tuning. L’exemple ci-dessous permet de comprendre la différence entre l’adaptation à une tâche et l’adaptation à un domaine :

L'adaptation à une tâche désigne la définition d’une consigne, présentée dans le prompt, pour la réalisation d'une tâche dans un domaine où le LLM dispose suffisamment de connaissances pour la réaliser. Tandis que l'adaptation à un domaine fait référence à l'apprentissage d'une tâche dans un domaine où le LLM ne possède pas suffisamment de contexte pour accomplir correctement la tâche. Par exemple, apprendre à coder en Python dans le cadre d'un projet relève de l'adaptation à une tâche. En effet, l'objectif est de construire un prompt donnant suffisamment de contexte au LLM afin qu’il génère des codes selon les pratiques de développement du projet. À l'inverse, lorsqu'un LLM doit apprendre un nouveau langage de programmation, l'entraînement ne se limite pas à la génération de code mais inclut également une compréhension approfondie du domaine, notamment de la syntaxe et du vocabulaire spécifiques à ce langage (absence de contexte préalable).

Bien que les LLMs aient été entraînés sur un large éventail de situations génériques, ils manquent souvent de connaissances pour des domaines spécialisés. Par exemple, GPT-3 peut exceller dans des échanges généraux mais fournit des réponses moins pertinentes, voire incorrectes (confabulations). C’est notamment le cas lorsqu’il est confronté à des termes techniques dans des domaines comme la médecine, le droit ou la finance. Dans ce cas, des techniques comme le RAG, le Chain of Thought ou le Prompt Engineering ne suffiraient pas pour apprendre une tâche précise dans un domaine spécialisé à cause de 2 principales limitations:

  • Techniques: Une fenêtre de contexte (context window) des LLMs trop petite. En effet, un LLM peut "garder en mémoire" qu’une quantité limitée de tokens (selon le modèle) pour comprendre une question et générer la réponse. Cela restreint donc la taille du contexte envoyé au LLM pour apprendre une nouvelle tâche.
  • Connaissances: Manque de savoir sur les vocabulaires, les acronymes ou encore les savoir-faire qui sont spécifiques à un domaine. Par exemple, si ce domaine est une entreprise, il faut voir le LLM comme un nouvel employé de cette entreprise qui ne connaît pas la culture. Il faut donc la communiquer ​afin que le LLM puisse interagir au mieux avec le contexte fourni pour répondre à une tâche.

Le fine-tuning permet donc de réentraîner le LLM sur un nouveau jeu de données afin qu’il acquiert les nouvelles connaissances liées au contexte/domaine spécifique. Afin d'éviter l'entraînement d'un modèle complet (full fine-tuning) et de réduire les coûts associés, PEFT constitue une solution efficace.

Algorithmes de PEFT

Le Parameter Efficient Fine-Tuning (PEFT) est un ensemble de méthodes consistant à ajuster seulement une petite fraction des paramètres du modèle pour l'apprentissage d'une tâche spécifique sur un nouveau jeu de données. Cela nécessite donc moins de ressources que l’entraînement complet de l’ensemble des paramètres du LLM (full fine-tuning). PEFT optimise ainsi l'utilisation des ressources en évitant l'entraînement complet du modèle. Pour cela, il existe 4 approches:

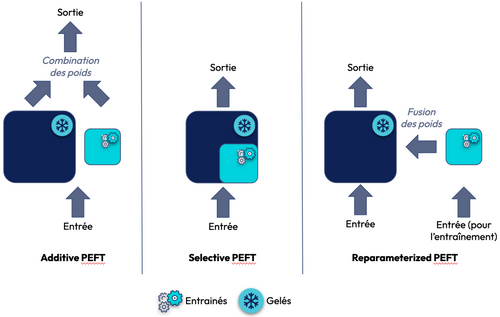
Représentation des approches des méthodes PEFTFigure 2: Approches des méthodes PEFT

  1. Additive PEFT: Ajout de paramètres ou couches supplémentaires au LLM, gel des poids existants et entraînement uniquement des nouveaux composants (paramètre(s) ou couche(s) ajoutée(s)). Bien que cette méthode permette de capturer plus efficacement les caractéristiques propres à une tâche, elle peut nécessiter un grand nombre de données pour éviter l’overfitting, ce qui peut augmenter la taille du modèle ainsi que le coût de calcul.
  2. Selective PEFT: Sélection et mise à jour uniquement d’un sous-ensemble des poids pré-entraînés les plus critiques pour la performance du modèle sur la tâche à apprendre. Les poids restants sont donc gelés, ce qui garantit qu'ils ne seront pas modifiés. Cette méthode est efficace d'un point de vue des ressources informatiques (hardware) utilisées, mais elle risque de ne pas utiliser pleinement la capacité du LLM lors de l’entraînement.
  3. Reparameterized PEFT: Ajout de matrices de faible rang pour mettre à jour les poids du modèle préexistant. Cette approche permet de trouver un équilibre entre l'adaptation et la préservation des connaissances du LLM mais est aussi efficace sur le plan informatique.
  4. Hybrid PEFT: Des combinaisons d'idées provenant de différentes méthodes sont souvent envisagées pour maximiser les performances, en tirant parti des points forts de chaque approche.

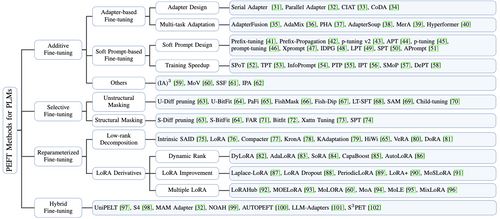
Liste des techniques PEFT réparties par approchesFigure 3: Techniques PEFT des LLMs (source: Han, Z., Gao, C., Liu, J., Zhang, J., & Zhang, S. Q. (2024, 21 mars). Parameter-Efficient Fine-Tuning for Large Models : A Comprehensive Survey. arXiv.org. https://arxiv.org/abs/2403.14608)

La figure 3 illustre les principales méthodes de PEFT et leurs variantes. Dans cette article, nous allons voir uniquement les algorithmes suivants :

  • Serial/Parallel Adapter: approche Additive Fine-Tuning
  • LoRA (Low-Rank Adaption): approche Reparameterized Fine-Tuning

1. Serial/Parallel Adapter

Ces techniques consistent à ajouter une ou plusieurs petite(s) couche(s) d'Adapter dans les blocs Transformer existants du LLM afin de ne pas ré-entraîner l’ensemble des paramètres. L'idée derrière PEFT est de geler les poids du modèle de base et de ne fine-tune que ces petites couches ajoutées, ce qui rend l'entraînement beaucoup plus rapide et léger.

Représentation d’un bloc de TransformerFigure 4: Représentation d’un bloc de Tran**sformer

Une couche d’Adapter est composée de réseaux de neurones compacts qui sont ajustés durant le fine-tuning spécifiquement pour la tâche à accomplir. Comme on peut le voir dans la figure ci-dessous, elle se compose d'une matrice de projection pour réduire la dimension (down-projection matrix), suivie d'une fonction d'activation non linéaire (ReLU), et d'une autre matrice de projection pour revenir à la dimension initiale (up-projection matrix). L’idée est que, au lieu de modifier tous les poids, l’Adapter va apprendre uniquement sur les patterns nécessaires pour modifier le comportement du LLM vers notre cible.

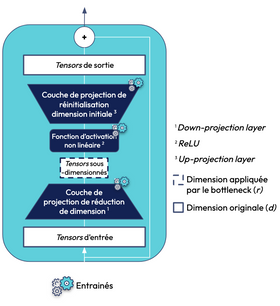
Représentation de la couche d'AdapterFigure 5: Représentation couche d'Adapter

La différence entre la couche d’un Adapter et celle de Feed Forward du bloc des Transformers est le paramètre bottleneck (goulot d’étranglement). Ce dernier a pour but de projeter les tensors d’entrée dans une dimension beaucoup plus petite, cela permet donc de réduire le nombre de paramètres à fine-tune pour l'apprentissage des nouvelles tâches. Une fois passés dans la fonction d’activation, les tensors sont projetés dans leur dimension initiale. Il existe également une autre différence entre les couches d’Adapter et de Feed Forward: la taille. En effet, la couche de l’Adapter est plus petite que celle du Feed Forward car elle possède une couche pour réduire la dimension de ses tensors d’entrée contrairement à celle du Feed Forward qui possède une couche cachée pour augmenter la dimension des tensors (cf. figures 4 & 5).

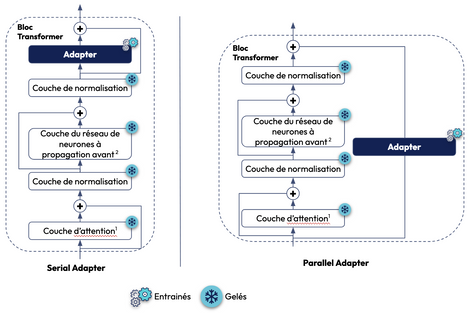
Il existe 2 approches concernant le positionnement de la couche d’Adapter (cf. figure ci-dessous):

  1. Serial Adapter: Chaque bloc de Transformer est amélioré par l'ajout d’une couche d’adapter après la couche d’attention (Multi-head attention) et la couche du réseau de neurones à propagation avant (Feed-forward network layer) respectivement
  2. Parallel Adapter: Contrairement à l’approche précédente où les couches d’Adapter sont séquentielles, ici, elles s'exécutent parallèlement à chaque bloc de Transformer

D’après une étude empirique de ce papier de recherche, la seconde approche présente de meilleurs résultats. Cette approche est notamment utilisée pour l’algorithme de LoRA.

Approches de l’AdapterFigure 6: Fonctionnement des approches de l’Adapter

2. LoRA (Low-Rank Adaptation):

LoRA permet d’approximer les matrices de poids du modèle, en particulier les matrices de projection (embeddings), par 2 matrices de faible rang. Cette approche vise à réduire le nombre de paramètres à ajuster lors du fine-tuning, tout en maintenant des performances similaires à celles obtenues avec l’ensemble des paramètres du modèle original. Plutôt que d’entraîner une matrice de grande dimension (dxk), LoRA entraîne 2 matrices de rang réduit dont le produit matriciel restitue une matrice de même dimension que celle des poids d'origine (cf. figure 7). Cela permet de diminuer le nombre de paramètres à entraîner, accélérant ainsi l’apprentissage. Les matrices de faible rang permettent de réduire le nombre de paramètres à fine-tune pour capturer de nouvelles informations sans avoir à réentraîner l’ensemble du modèle. Une fois ces 2 matrices multipliées, le résultat du produit matriciel est additionné avec la matrice des poids du modèle préexistant.

Pour illustrer, dans le cas où le LLM à fine-tune possède une matrice de poids de dimension 4096x4096, cela représente 16 777 216 paramètres à entraîner pour une seule couche. Si l’on applique LoRA avec un rang égale à 8 (r=8), nous aurons une première matrice de dimension 8 x 4096 puis la seconde de 4096 x 8. Cela représente 65 536 paramètres, ce qui représente 256 fois moins de valeurs à entraîner pour une seule couche d’attention.

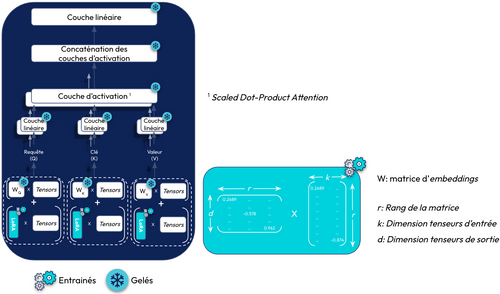
Représentation du fonctionnement de LoRAFigure 7: Représentation du fonctionnement de LoRA

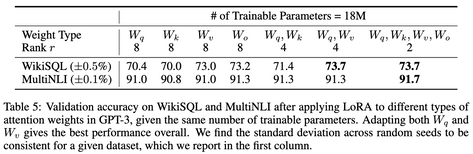
Dans le papier de recherche de la méthode LoRA, un test empirique de cette méthode a été réalisé sur GPT-3 démontrant que la méthode LoRA est plus efficace lorsqu’on l’applique sur les matrice de poids des requêtes (Q) et clés (K) (cf.figure ci-dessous).

Résultats du test empirique de la méthode LoRA sur GPT-3Figure 8: Résultats du test de la méthode LoRA sur GPT-3 (source: Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., Wang, L., & Chen, W. (2021, 17 juin). LoRA : Low-Rank Adaptation of Large Language Models. arXiv.org. https://arxiv.org/abs/2106.09685)

Optimisation des algorithmes

Malgré le fine-tuning d’une petite fraction des paramètres du LLM, les différents algorithmes de PEFT demandent beaucoup de ressources en mémoire durant l'entraînement. Cela est d’autant plus le cas lorsqu’il s’agit d’un LLM avec des centaines de millions voire des milliards de paramètres, ce qui peut donc générer de la latence de traitement et des pics de mémoire des GPUs. En effet, on retrouve un système auto-régressif dans l’architecture des Transformers. Ils génèrent un token à la fois en se basant sur le contexte précédent. Cela implique une répétition des calculs ou l'utilisation d’un cache mémoire du GPU à chaque étape, ce qui peut ralentir l’inférence, notamment sur de longs contextes. Il existe des stratégies visant à réduire davantage la complexité de calcul des différents algorithmes PEFT (cf. figure ci-dessous). Cela permet d’améliorer les performances du modèle tout en minimisant la consommation de ressources lors de l’entraînement mais également lors de l’inférence.

Liste des méthodes d'optimisation des algorithmes PEFTFigure 9: Méthodes d’optimisation des algorithmes PEFT (source: Han, Z., Gao, C., Liu, J., Zhang, J., & Zhang, S. Q. (2024, 21 mars). Parameter-Efficient Fine-Tuning for Large Models : A Comprehensive Survey. arXiv.org. https://arxiv.org/abs/2403.14608)

Dans cet article, nous allons parler uniquement de la quantification avec la stratégie QLoRA.

Quantized LoRA (QLoRA) :

QLoRA est une version étendue de LoRA conçue pour améliorer l'efficacité de la mémoire du fine-tuning des poids originaux du LLM. Généralement, les paramètres de la matrice de poids du LLM préexistant sont stockés en float de précision 16 ou 32 bits. Or, QLoRA utilise diverses techniques pour réduire considérablement l'empreinte mémoire. Cela permet donc de charger et ajuster des LLMs sur du matériel GPU plus modeste, grâce à un besoin en mémoire et stockage réduit, sans impact significatif sur les performances.

Représentation des floats dans une mémoire

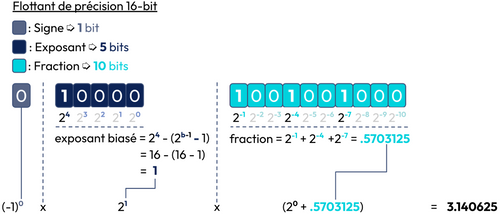
Un float est encodé en bits dans la mémoire, souvent selon la norme IEEE 754. Cet encodage représente le float en trois fonctions (cf. figure 10) :

  • Signe: Indique si le nombre est positif (0) ou négatif (1).
  • Exposant: Représente la puissance de 2 pour positionner la virgule
  • Fraction: Contient les chiffres après la virgule (valeur significative du nombre en bits)

Présentation fonctionnement du stockage d’un float dans la mémoireFigure 10: Présentation fonctionnement du stockage d’un float dans la mémoire

Comme on peut le voir sur la figure ci-dessous, la plage de valeurs représentée dans une mémoire (RAM ou VRAM) augmente avec le nombre de bits disponibles. Autrement dit, la quantité de mémoire dont votre machine a besoin pour stocker une valeur donnée augmente avec le nombre de bits disponibles. Cela veut donc dire que pour les LLMs qui présentent des milliards de paramètres, charger ses poids en mémoire avec un nombre de bits élevés (16 bits ou 32 bits) demande beaucoup de ressources mémoires (à l'entraînement et à l’inférence).

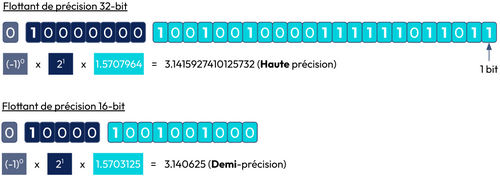
Représentation du nombre pi en bitsFigure 11: Tentative de représentation du nombre pi en float de précision 16 et 32 bits

Il est donc nécessaire de pouvoir minimiser le nombre de bits pour représenter les paramètres de votre LLM.

Pour garder une performance quasi intacte des LLM avec peu de ressources en mémoire, QLoRA utilise 3 techniques (en plus de l'algorithme de LoRA):

  1. 4-bit NormalFloat Quantization: Nouveau type de flottant optimal pour les valeurs suivant une distribution normale.
  2. Double Quantization: Une quantification hiérarchique c’est-à-dire que les facteurs de quantification eux-mêmes sont quantifiés pour économiser encore plus de mémoire.
  3. Paged Optimizer: Une façon de gérer dynamiquement l’utilisation de la mémoire GPU et CPU, surtout pendant le fine-tuning.

4-bit NormalFloat Quantization (NF4)

La quantification (quantization) permet de réduire le nombre de bits représentant des valeurs tout en réduisant très peu voire pas du tout la précision du modèle. Voilà une définition de la quantification donnée par Bryan Clark d’IBM.

“La quantification est le processus qui consiste à réduire la précision d'un signal numérique, généralement d'un format de haute précision à un format de plus faible précision”

Définition de la quantification donnée par Bryan Clark (IBM)

Avec la quantification, on souhaite donc réduire le nombre de bits tout en continuant à représenter avec précision les valeurs des poids originaux du LLM. Toutefois, une quantification linéaire i.e transformer les poids (chargées en FP32) en INT8 dans notre cas pose problème comme on peut le voir à travers ces 2 exemples:

  • Il se peut que la matrice de poids présente des valeurs aberrantes comme le montre la figure ci-dessous. En effet, lorsque l’on a des valeurs aberrantes, 2 valeurs voisines de grande précision (c’est-à-dire la distance entre les 2 valeurs voisines est faible) sont identiques une fois quantifiée, ce qui pose problème pour le fine-tuning.
  • Lorsque la plage dynamique est trop petite pour les valeurs à quantifier, 2 valeurs voisines perdent en précision (autrement dit les 2 valeurs deviennent plus proches après la quantification) ce qui pose également problème pour la matrice de poids du LLM qui comportent les valeurs de précision comme elles sont proches de 0. Cela nuit donc au fine-tuning.

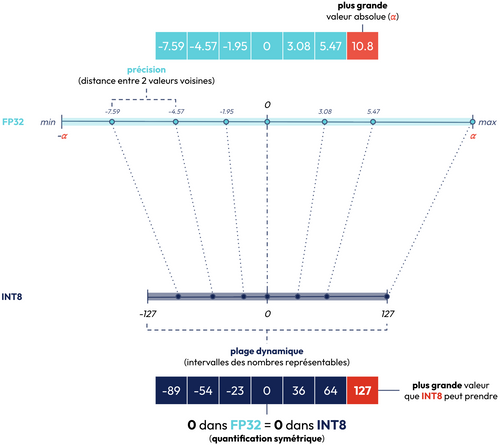
llustration d’une quantification linéaireFigure 12: Illustration d’une quantification linéaire

Donc au lieu d’appliquer une quantification linéaire des valeurs des poids, QLoRA va utiliser la technique de 4-bit NormalFloat Quantization (NF4). Cette dernière utilise la block-wise quantification (quantification par blocs). Au lieu de faire correspondre tous les poids du LLM dans un seul bloc i.e projeter un tensor (au sens physique) de la matrice des poids sur une seule plage dynamique, des blocs supplémentaires (avec la même plage dynamique) sont créés afin de découper le tensor en plusieurs blocs pour permettre la quantification de valeurs de poids similaires.

NF4 se base sur la quantification par quantile dont l’idée serait que chaque bloc représente un quantile du tensor, sauf que le problème est que le calcul du quantile est trop lourd d’un point de vue computationnel. N’étant pas possible, NF4 s’appuie sur la propriété des réseaux de neurones: la distribution normale des poids. Cette propriété permet de calculer une approximation (avec une erreur faible) des quantiles en fonction de leur densité relative des poids. Cela permet non seulement de réduire drastiquement les besoins en mémoire mais aussi les problèmes liés aux valeurs aberrantes.

Voici les étapes de l’implémentation de la quantification NF4 :

  1. Découpage en blocs : Les poids sont groupés (ex: taille 64 ou 128) pour une quantification.
  2. Normalisation des blocs : Les valeurs des poids étant centrées sur 0 de par sa propriété, chaque bloc est normalisé (entre -1 et 1) en étant divisé par la valeur absolue maximum du bloc.
  3. Quantification des blocs : Chaque poids normalisé du bloc est mappé à l’une des 16 valeurs du NF4 dont les valeurs correspondent aux approximations des quantiles (cf. figure 13). Il est remplacé par l’indice de la valeur dont le il est plus proche en valeur absolue. Pour information, on constate que la quantification n’est pas symétrique pour ces 2 raisons:
    • Les intervalles entre les valeurs représentables du NF4 ne sont pas répartis uniformément autour de 0
    • La valeur 0 ne possède pas de valeur quantifiée exacte, c’est-à-dire 0 avant quantification n’est pas égale au 0 dans NF4 (valeur comprise dans un intervalle).

La raison pour laquelle on applique une quantification asymétrique est qu’une quantification symétrique à 4 bits pose problème. En effet, on n’a pas toujours une représentation exacte de zéro, ce qui est important pour quantifier sans erreur des éléments nuls, comme par exemple le padding.

4. Stockage : On stocke par bloc le facteur d’échelle (scale) et les indices 4-bit (permettant de retrouver quels facteurs correspondant à chaque bloc) en float16.

Valeurs représentables de la plage dynamique du NF4Figure 13: Valeurs représentables de la plage dynamique du NF4

NF4 est appliqué uniquement sur les poids gelés de la couche d'attention du LLM à fine-tune, les poids fine-tuned dans la couche LoRA restent en bfloat16 (Brain Floating Point 16). C’est un format de nombre à virgule flottante sur 16 bits, conçu par Google, dont l’objectif est de réduire la mémoire et le coût de calcul tout en conservant une bonne précision numérique pour l'entraînement de réseaux de neurones. Une fois le fine-tuning de LoRA terminé, les valeurs de la matrice des poids gelés du LLM sont ensuite dé-quantifiées pour l'additionner avec la matrice des poids fine-tuned par LoRA afin de mettre à jour les valeurs des poids de la couche d’attention.

Lorsque QLoRA applique le 4-bit NormalFloat Quantization après l’entraînement du LLM, c’est ce qu’on appelle le Post Trained Quantization (PTQ). En effet, ici on applique la quantification sur la matrice des poids gelés ce qui génère une perte plus faible sur les valeurs des poids en haute précision (ex: FP32). NF4 permet de diviser la consommation mémoire d’une valeur de poids d’un LLM jusqu’à 8 en passant de 32 bits à 4 bits (cas où les valeurs initiales des poids sont chargées en FP32). À noter également que cette technique est également utile pour l'inférence car les LLMs sont quantifiés et donc plus petits en taille, ce qui nécessitent donc moins de VRAM (Video Random Access Memory: stockage temporaire des données utilisé par le processeur graphique pour la gestion des activités du GPU). Cela est essentiel pour déployer de très grands modèles sur du matériel limité. À l’inverse, NF4 peut être appliqué pendant l’entraînement du LLM, c’est ce qu’on appelle le Quantization-Aware Training (QAT). L’idée est de fine-tune le modèle en simulant la quantification NF4 pendant l'entraînement. Cette approche permet au LLM d'apprendre à compenser la perte d'information due à la quantification afin de minimiser les erreurs de quantification contrairement au PTQ.

En pratique, la quantification NF4 (cas PTQ) fonctionne en divisant les poids du modèle en blocs (de taille 64 par exemple). Chaque bloc possède une constante de quantification (scale) propre, nécessaire pour re-transformer les valeurs quantifiées. Toutefois, ces constantes, souvent stockées en 32 bits, occupent elles aussi de la mémoire. Cela peut devenir un surcoût important à mesure que la taille du modèle augmente. Même avec NF4, les paramètres (comme le scale) par bloc représentent un poids mémoire non négligeable à grande échelle. C’est la raison pour laquelle la Double Quantization est utilisée dans la stratégie QLoRA.

Double Quantization

C’est un processus consistant à quantifier les constantes de quantification (scale) afin de réduire davantage l'empreinte mémoire. Bien qu'une petite taille de bloc soit nécessaire pour une quantification 4 bits précise, elle entraîne également une surcharge mémoire considérable. En effet, dans le cas où nos poids ont été quantifiés par des blocs de taille 64 et que les constantes de quantification sont stockées en 32 bits, nous avons en moyenne 0.5 bit à stocker en mémoire en plus pour chacun des 64 paramètres. Cela n’est pas négligeable lorsque l’on sait qu’on applique la quantification sur plusieurs milliards de paramètres et que chacun des blocs peut avoir une constante de quantification avec une valeur différente.

Pour faire ça, on applique une quantification par bloc. La différence ici est que nous utilisons des blocs de taille 256 et que ces nouvelles constantes de quantification sont stockées en 8-bits. Si l’on reprend maintenant notre bloc de 64 paramètres, on constate qu’en moyenne 0.127 bit (8/64 + 32/(64 x 256) = 0.127) est stocké en plus pour chacun des paramètres, ce qui représente une diminution de 0.373 bit soit près de 75%. Passage du 32 bits au 8 bits permet de diviser par 4 la mémoire (baisse 75%)

La Double Quantization permet en effet de réduire la taille du modèle chargé en GPU mais il reste cependant un problème. Lors du fine-tuning du LLM, l’optimizer doit gérer des données dynamiques (comme les gradients, les historiques de mises à jour, etc.) en évitant les pics de mémoire, c’est justement l’intérêt du Paged Optimizer. Ce dernier optimise l'utilisation de la mémoire globale (GPU + CPU), ce qui permet d’avoir un pipeline d’entraînement plus efficace et mieux équilibré.

Paged Optimizers

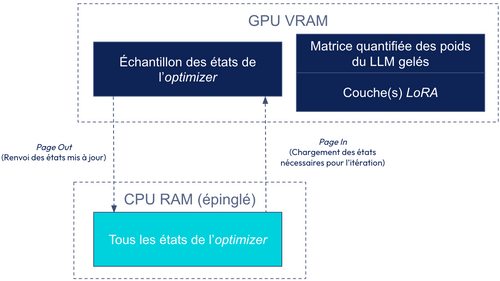
Le Paged Optimizer est une technique permettant de gérer les pics de mémoire lors de l'entraînement de modèles quantifiés. Dans le cas du LLM, les gradients peuvent provoquer des pics de consommation de mémoire qui dépassent la capacité de la mémoire GPU disponible. Pour résoudre ce problème, les Paged Optimizers divisent les optimizers en "pages" plus petites, qui sont traitées et stockées de manière séquentielle, réduisant ainsi la charge mémoire à tout moment.

Initialement, les algorithmes d’optimisation des hyper paramètres, tels que la descente du gradient ou Adam, chargeaient tous les états de l’optimizer (déplacements dans le gradient) de tous les poids sur le GPU. Tandis que Paged Optimizer propose de charger dans le GPU uniquement les états nécessaires pour l’itération et le reste est stocké dans le CPU.

Cette approche permet de maintenir une utilisation efficace de la mémoire du GPU.

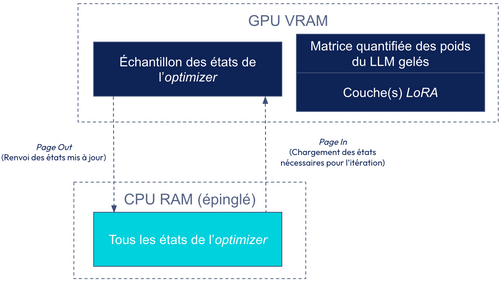
Fonctionnement du Paged OptimizerFigure 14: Fonctionnement du Paged Optimizer

Prenons l’exemple de l’optimizer Adam. Pour rappel, l’algorithme stocke pour chaque poid fine-tuned 3 paramètres:

  • Le gradient
  • Le 1er moment: moyenne des gradients appelé aussi momentum (estimation de la tendance)
  • Le 2nd moment: moyenne des carrés des gradients (estimation de la variance)

Les 1er et 2nd moments permettent de mettre à jour l’optimizer en prenant des pas plus ou moins importants pour les poids selon si le gradient présente du bruit (ou non) ou est éparse (ou non). Les états de l’optimizer peuvent être chargés en haute ou basse précision mais souvent ils sont chargés en haute précision afin de permettre des pas de plus en plus petits dans la gradient.

Si l’on revient sur le Paged Optimizer, voici les 5 étapes de son fonctionnement:

  1. **Quantification des états de l’**optimizer (facultatif): Souvent, les Paged Optimizers quantifient également les états de l’optimizer eux-mêmes (par exemple en précision 8 bits), ce qui réduit immédiatement leur taille intrinsèque. Mais selon la quantification appliquée aux états, cela peut affecter la stabilité de l’optimizer.
  2. Stockage des états de l’optimizer dans le CPU: La majorité des états de l’optimizer résident en mémoire CPU épinglée. Pour information, une mémoire épinglée permet des transferts de données plus rapides entre le CPU et le GPU.
  3. **Pagination de l’état de l’**optimizer actif (Page In): Seuls les états de l’optimizer nécessaires pour le calcul en cours, c’est-à-dire pour les paramètres impliqués dans la mise à jour de l’optimizer du mini-batch sont transférés de la RAM du CPU vers la VRAM du GPU juste avant d’être utilisés.
  4. **Mise à jour de l’**optimizer sur le GPU: Le calcul de l’étape de l’optimizer s’effectue sur le GPU en utilisant les états chargés dans la VRAM du GPU.
  5. **Mise à jour de l’état de l’**optimizer dans le CPU (Page Out): Les états mis à jour peuvent être renvoyés vers la RAM du CPU.

Conclusion

En résumé, nous avons exploré le Parameter-Efficient Fine-Tuning (PEFT), un ensemble de techniques (additive, reparameterized, selective, hybride) permettant d’adapter un LLM à une tâche spécifique en ne modifiant qu’une petite fraction de ses paramètres. Dans cet article, nous nous sommes focalisés sur deux méthodes phares : Adapter et LoRA.

La méthode Adapter consiste à insérer des couches supplémentaires au sein des blocs Transformer. Ces couches apprennent uniquement les ajustements nécessaires pour orienter le comportement du modèle vers la tâche cible. LoRA consiste également à insérer de nouvelles couches mais qui reposent sur une décomposition des matrices de poids à partir de matrices de faible rang, permettant de réduire considérablement le nombre de paramètres à entraîner, et donc le coût computationnel.

Cependant, malgré sa grande efficacité en termes de performances, LoRA peut présenter des limitations en matière de consommation mémoire. C’est dans ce contexte qu’intervient QLoRA, une amélioration de LoRA visant à optimiser l’usage de la mémoire tout en conservant la qualité des résultats. Elle s’appuie sur trois techniques clés :

  • 4-bit NormalFloat Quantization : un format de flottants quantifiés basé sur une distribution normale, permettant de réduire la mémoire GPU requise ;
  • Double Quantization : une quantification secondaire des constantes de quantification, pour un gain mémoire supplémentaire ;
  • Paged Optimizer : une gestion mémoire intelligente entre GPU et CPU lors de la mise à jour des gradients, afin de prévenir les erreurs de type out-of-memory.

Ainsi, PEFT, et en particulier QLoRA, permet aujourd’hui de fine-tuned des LLMs de manière bien plus accessible, aussi bien en termes de ressources que de coûts, tout en maintenant des performances proches du fine-tuning complet.

Sources