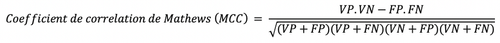Données déséquilibrées, que faire ?
Dans un problème de classification, il arrive souvent d’avoir des datasets très déséquilibrés. On parle d’un dataset déséquilibré lorsque le ratio des observations d’une classe par rapport à l’ensemble des observations est très faible.
Cette notion de déséquilibre de classes est relativement fréquente dans plusieurs secteurs comme le secteur médical ou le secteur bancaire et elle est problématique lorsqu’elle n’est pas traitée.
En adoptant une approche naïve de classification, autrement une approche qui ne prend pas en compte ce déséquilibre des classes, on risque fortement de biaiser le modèle. Ainsi, dans le cas de détection des maladies rares ou de détection de fraude à titre d’exemple, le risque d’une approche naïve de classification est de prédire des patients potentiellement malades comme étant en bonne santé ou des transactions frauduleuses comme étant tout à fait licites.
Cet article vise à présenter un panel de techniques utilisées pour résoudre ce problème de déséquilibre de classes. Nous allons y aborder cette notion dans le cadre de la classification binaire de données structurées uniquement et nous allons y explorer les différentes techniques à travers un exemple. Le code est disponible sur Github.
On choisit, comme exemple, le dataset d’une compagnie d’assurance automobile brésilienne dont le but est de pouvoir adapter ses prix et ses offres en fonction du client. L’objectif est de prédire si un client est un bon conducteur ou non; un mauvais conducteur étant une personne qui va faire une réclamation dans l’année courante.
Dans le dataset d’entraînement, on considère qu’un mauvais conducteur est un positif et qu’un bon conducteur est un négatif. Autrement, un positif est un client ayant déjà fait une réclamation et un négatif est un client n’en ayant jamais faite. Ultimement, en classifiant sa population de clients dans le dataset de test, la compagnie vise à :
- Avoir le minimum de faux négatifs (Prédire un conducteur comme étant bon alors qu’en réalité il est mauvais)
- Prédire le maximum de vrais positifs (Prédire un conducteur comme étant mauvais quand c’est vraiment le cas)
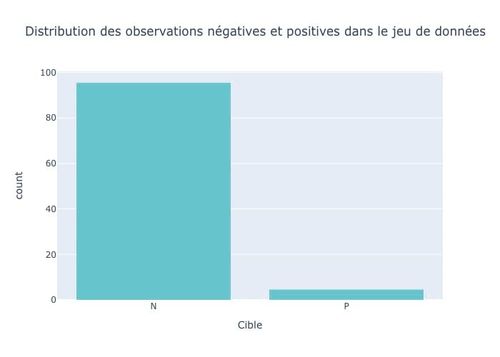
Pour le dataset choisi, on a 95% d’observations négatives :
Figure 1 : Distribution des clients d’une assurance automobile issus du dataset « Porto Seguro’s Safe Driver Prediction » sur Kaggle
Adopter une approche naïve ?
Pour répondre à la problématique de la compagnie d’assurance, on peut d’abord commencer par une approche naïve de classification. On choisit d'entraîner un LightGBM et un Stochastic Gradient Descent sur les données. Les deux modèles reposent sur la descente de gradient. L’objectif ici n’est pas de comparer les deux modèles, mais plutôt de regarder leurs comportements lorsqu’on a une situation de déséquilibre des classes.
On choisit d’abord d’utiliser l’accuracy, comme métrique d’évaluation. Elle indique le taux de bonnes prédictions réalisées par le modèle. En définissant la matrice de confusion du modèle par :
| Classe Réelle | |||
| + | - | ||
| Classe Prédite | + | Vrais Positifs (VP) | Faux Positifs (FP) |
| - | Faux Négatifs (FN) | Vrais Négatifs (VN) |
L’accuracy est ainsi définie comme suit :
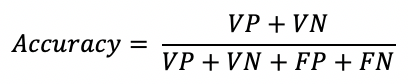
En termes d’accuracy, le LGBM réalise 95.4% et le SGD réalise 95.2%. Au premier abord, les modèles semblent avoir une bonne performance. Mais en regardant un peu plus dans le détail la matrice de confusion, on remarque que les deux modèles prédisent quasi toujours des observations négatives.
| Classe Réelle | |||
| + | - | ||
| Classe Prédite | + | 0 | 2 |
| - | 576 | 11916 |
| Classe Réelle | |||
| + | - | ||
| Classe Prédite | + | 0 | 0 |
| - | 576 | 11918 |
Figure 2 : Matrices de confusion des deux modèles entraînés, en haut celle du Light GBM, en bas celle du Stochastic Gradient
A titre de comparaison, un modèle naïf qui consiste à prédire toujours des observations négatives a une accuracy de 95% dans notre cas puisqu’il y a 95% d’observations négatives dans le dataset de test. Les deux modèles sont alors presque aussi bons que ce modèle naïf. Leur performance en termes d’accuracy n’est pas pertinente dans ce contexte et ne permet pas de réellement évaluer le modèle.
Choisir la métrique la plus pertinente d’un point de vue métier
Il est nécessaire de bien choisir la métrique d’évaluation. Il faut que cette métrique soit d’abord cohérente avec les objectifs du métier mais aussi pertinente pour répondre à sa problématique :
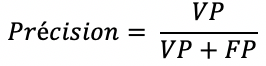
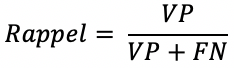
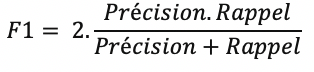
Le rappel indique la capacité du modèle à prédire correctement tous les positifs et la précision indique la capacité du modèle à ne prédire que les positifs. Ce sont des métriques pertinentes à utiliser quand on s’intéresse principalement à la classe positive. Néanmoins, elles sont asymétriques. Autrement, si on inverse la classe positive et la classe négative, elles n’auront plus la même valeur.
De même, le score F1 est très intéressant quand il existe un double enjeu et qu’on cherche à avoir à la fois un bon rappel et une bonne précision. Il s’agit d’une moyenne des deux métriques. Toutefois, ce score moyenne de façon égale la précision et le rappel et il arrive parfois que le métier s’intéresse à un aspect du problème plus que l’autre. Dans le cas d’une classification multiclasse, le score F1 existe aussi sous d’autres formes.
Si on s’intéresse à la performance du modèle de façon globale, le coefficient de corrélation de Matthews ou le MCC reste la meilleure métrique à utiliser. Concrètement, si on considère que la classe prédite et la classe réelle sont deux variables binaires, le MCC représente la corrélation entre ces deux variables. C’est une métrique qui est symétrique et insensible au déséquilibre de classes.
L’ensemble des métriques que nous utilisons dans cet article n’est pas une liste exhaustive. On fait le choix d’évaluer uniquement celles-ci. Notre approche naïve de classification nous donne les résultats suivants :
| Modèle | Accuracy | Précision | Rappel | F1-Score | MCC |
| LGBM | 95.4% | 0% | 0% | 0% | -0.002 |
| SGD | 95.2% | 4.5% | 0.2% | 0.3% | -0.001 |
On voit bien que sans traiter cette contrainte de déséquilibre des données, les deux modèles ont une très faible performance qu’il s’agisse de la précision, du rappel, du score F1 ou encore du MCC.
Regardons maintenant les techniques les plus communément utilisées pour contourner le problème. On peut les catégoriser en deux grandes familles :
- Techniques se basant sur l’amélioration du jeu de données
- Techniques se basant sur l’amélioration de la phase de modélisation
On précise qu’il ne s’agit pas d’une liste exhaustive de techniques.
Ré-échantillonner le jeu de données
Le ré-échantillonnage est l’une des méthodes les plus régulièrement utilisées pour résoudre ce problème.
- Sur-Échantillonnage :
Lorsque le dataset n’est pas assez grand, on peut sur-échantillonner les observations associées à la classe la moins prépondérante. On peut générer de nouveaux échantillons par répétition de façon aléatoire ou en s’appuyant sur des méthodes un peu plus sophistiquées comme SMOTE ou ADASYN.
SMOTE pour Synthetic Minority Over-Sampling Technique consiste à sur-échantillonner en se basant sur les proches voisins de la classe minoritaire.
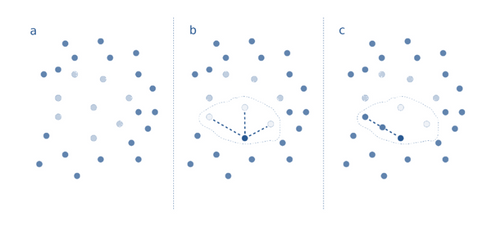
Figure 3 : [4] Graphique représentant les différentes étapes de la méthode SMOTE. Dans a, les points bleus clairs représentent les observations de la classe minoritaire et les points bleus foncés représentent les observations de la classe majoritaire. Dans b, le périmètre délimité représente un point de la classe minoritaire et ses trois proches voisins. Dans c, le périmètre délimité représente le même point de la classe minoritaire, ses trois proches voisins et le point synthétique créé
- D’abord, on choisit une observation de la classe minoritaire et on sélectionne aléatoirement un de ses proches voisins appartenant à la même classe en utilisant la distance euclidienne (Étape b, Figure 2)
- Ensuite, on calcule la différence pour chaque feature et on la multiplie par un nombre aléatoire entre 0 et 1.
- Finalement, on ajoute le résultat à l’observation choisie pour obtenir un nouveau point (Étape c, Figure 2).
Le procédé est par la suite réitéré pour chaque point de données de la classe minoritaire.
SMOTE est une technique qui est utilisée avec des données continues uniquement. Pour les données catégorielles, il existe une version adaptée appelée SMOTENC pour SMOTE Nominal Continous.
SMOTE présente tout de même quelques faiblesses, quant à la logique de sur-échantillonage utilisée. D’une part, il ne prend pas en compte les exemples voisins pouvant provenir de la classe majoritaire. Les observations synthétiques créées peuvent donc se chevaucher avec d’autres observations de la classe majoritaire.
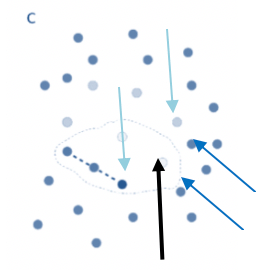
Figure 4 : Graphique une étape intermédiaire de la méthode SMOTE, la flèche noire pointant vers l’observation choisie de la classe minoritaire, les flèches bleues claires pointant vers ses proches voisins de la même classe, les flèches bleues foncées pointant vers ses proches voisins de la classe majoritaire
D'une autre part, la génération de plusieurs observations synthétiques risque de générer ce qui est en réalité du bruit supplémentaire dans le jeu de données, ce qui pourrait éventuellement biaiser le modèle.
ADASYN pour ADAptive SYNthetic est une version améliorée de SMOTE. Au lieu de générer le même nombre d’observations synthétiques pour chaque observation de la classe minoritaire choisie, nous allons adapter le sur-échantillonnage à la densité de distribution des observations de la classe minoritaire. Concrètement, ADASYN génère plus d’échantillons synthétiques dans les régions de l’espace des features où la densité des observations minoritaires est faible et moins d’échantillons dans les régions où la densité est plus élevée.
Pour notre exemple, on applique SMOTE et on ré-entraîne les modèles en optimisant les hyperparamètres.
from imblearn.over_sampling import SMOTENC
# Choix de la taille du nouveau dataset
distribution_of_samples = {0:119261, 1:20000}
# Sur-Echantillonnage en utilisant la méthode SMOTE
smote = SMOTENC(categorical_features=index_cat, sampling_strategy = distribution_of_samples, random_state = 0)
X_over_sample, y_over_sample = smote.fit_sample(X,y)
On obtient les résultats suivants :
| Modèle | Accuracy | Précision | Rappel | F1-Score | MCC |
| LGBM | 95.6% | 96.7% | 5% | 9.6% | 0.22 |
| SGD | 95.2% | 9.7% | 0.5% | 1% | 0.012 |
- Sous-Échantillonnage :
Lorsqu’au contraire le nombre d’observations dans le dataset est assez important, on a la possibilité de sous-échantillonner les observations associées à la classe la plus prépondérante. On peut réaliser un sous-échantillonnage de façon aléatoire mais on peut également utiliser d’autres techniques telles que NearMiss.
NearMiss vise à séparer les observations correspondantes à des classes différentes. Son principe est de supprimer les observations de la classe majoritaire lorsque des observations associées à des classes différentes sont proches l’une de l’autre.
from imblearn.under_sampling import NearMiss
# Choix de la taille du nouveau dataset
distribution_of_samples = {0:60000, 1:5600}
# Sous-Echantillonnage en utilisant la méthode NearMiss
nearmiss = NearMiss(sampling_strategy = distribution_of_samples)
X_under_sample, y_under_sample = nearmiss.fit_sample(X,y)
En appliquant NearMiss à notre exemple, on a les résultats suivants :
| Modèle | Accuracy | Précision | Rappel | F1-Score | MCC |
| LGBM | 91.6% | 10.6% | 10.9% | 10.8% | 0.06 |
| SGD | 93.8% | 7% | 2.8% | 4% | 0.015 |
Qu’il s’agisse d’appliquer un sous-échantillonnage ou un sur-échantillonnage, on voit bien que les modèles ont de meilleures performances en termes de rappel, de précision, de score F1 ou de MCC.
De façon générale, l'utilisation d'une méthode plutôt que l'autre dépend de la taille de l'ensemble d'apprentissage.
- On peut aussi utiliser des méthodes hybrides de ré-échantillonnage qui combinent le sur échantillonnage de la classe minoritaire et le sous-échantillonnage de la classe majoritaire.
Utiliser le Cost-Sensitive Learning
Le Cost-Sensitive Learning peut également être une solution au problème de déséquilibre de classes. C’est un type d’apprentissage qui prend en compte les coûts d’une mauvaise classification.
En effet, au cours de l’étape d’apprentissage, on peut attribuer des poids aux observations et le poids de chaque observation sera d’autant plus important que la classe de celle-ci est minoritaire. Le principe est de redéfinir la fonction de coût du modèle en tenant compte de ces poids.
On rappelle que la fonction de coût est une fonction qui calcule l’erreur entre les valeurs réelles et les valeurs prédites lors de l’apprentissage, l’objectif de l’apprentissage étant d’ailleurs de trouver les paramètres du modèle qui la minimisent.
Par exemple, pour plusieurs modèles de boosting tels que XGBoost, Light GBM ou encore Catboost, redéfinir la fonction de coût du modèle en prenant en compte la distribution des observations dans le jeu de données d’entraînement revient tout simplement à définir le paramètre scale_pos_weight. On ne s’attarde pas dans cet article sur l’aspect théorique du Cost-Sensitive Learning mais pratiquement, adopter un apprentissage « sensible au coût » se traduit par le choix de l’hyperparamètre scale_pos_weight ou ses équivalents pour d’autres modèles de ML tel le class_weight pour le SGD.
import lightgbm as lgb
lgb_classifier = lgb.LGBMClassifier(boosting_type='goss',
max_depth=5,
learning_rate=0.1,
n_estimators=1000,
subsample=0.8,
colsample_bytree=0.6,
scale_pos_weight = Number_of_negatives/Number_of_positives)
classifier = lgb_classifier.fit(X_train, y_train, verbose=0)
y_pred = classifier.predict(X_test)
De façon générale, il est recommandé de prendre comme valeur, pour le scale_pos_weight, le ratio des observations négatives par rapport aux observations positives. Néanmoins, on peut très bien chercher à l’optimiser. Pour notre exemple, on a les résultats suivants :
| Modèle | Accuracy | Précision | Rappel | F1-Score | MCC |
| LGBM | 85.6% | 7.9% | 19.8% | 11.3% | 0.06 |
| SGD | 90.3% | 9.6% | 13.4% | 11.2% | 0.06 |
On peut ainsi voir que le Cost-Sensitive Learning améliore aussi les performances du modèle.
Utiliser l’Ensemble Learning
- Le principe de l’ « Ensemble Learning » est de moyenner les prédictions de différents modèles. Dans le cas de déséquilibre de classe, une idée serait d’entraîner les différents modèles sur des différents jeux de données avec le même ratio positifs/négatifs ré-échantillonnés à partir du jeu de données initial.
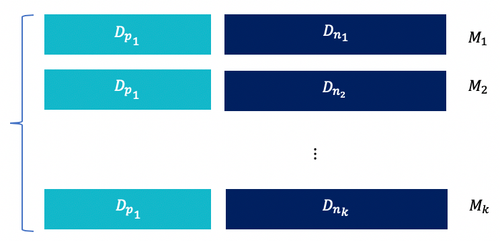
Figure 5 : Division de l'ensemble d'apprentissage en k sous-ensembles différents de même taille entraînés par k modèles M différents; chaque sous-ensemble se constituant du même ensemble des observations positives et d'un sous-ensemble des observations négatives
Les Dp1 et les D~ni ~ représentent respectivement les observations positives et les observations négatives. Les M~i ~ représentent les modèles appris respectivement sur les jeux de données Di ={Dni, Dp1}.
Pour notre exemple, on crée 5 sous-ensembles d’observations négatives en ré-échantillonnant l’ensemble d’observations négatives initial et en le divisant par 5. Ainsi, on obtient cinq jeux de données différents.
Ensuite, on entraîne 5 modèles différents, chacun sur un des datasets. La prédiction finale est une prédiction « moyenne » des 5 modèles :
| Modèle | Accuracy | Précision | Rappel | F1-Score | MCC |
| LGBM | 93.5% | 11.5% | 0.6% | 0.08% | 0.05 |
| SGD | 94.5% | 14% | 3.6% | 5.8% | 0.05 |
Encore une fois, bien que la performance des deux modèles soit faible en termes de rappel et de précision, elle reste tout de même meilleure que lorsqu’on ne gère pas le déséquilibre de classes.
- Toujours dans la même optique, une autre idée serait d’entraîner les différents modèles sur des jeux de données ré-échantillonnés mais cette fois, avec des ratios positifs/négatifs différents.
Utiliser la One-Class-Classification
Parfois, lorsque le pourcentage des observations d’une classe est extrêmement faible comme dans le cas de la détection de fraude, il est plus judicieux de considérer le problème comme un problème de One Class Classification.
Ce type de classification consiste à apprendre sur un jeu de données contenant uniquement une seule classe d’observations. Au cours de la phase de test, on cherchera à déterminer si une nouvelle observation ressemble à la population d’observations sur lesquelles le modèle a été entraîné ou si à l’inverse elle peut être considérée comme un outlier et donc appartenir à l’autre classe.
En quelques mots, deux familles de solutions existent pour les problèmes de One Class Classification :
- Les méthodes de densité dont le but est d’estimer la densité de probabilité de l’espace des observations et considérer les queues des distributions comme étant des observations appartenant à la classe minoritaire.
- Les méthodes de frontière telles que le One Class SVM dont l’objectif est d’estimer la frontière de la classe majoritaire et de considérer ce qui est extérieur à cette frontière comme des observations de la classe minoritaire.
Conclusion
Dans un problème de classification, il n’est pas rare que la modélisation soit contrainte par le déséquilibre des classes. Il est donc indispensable de pouvoir y faire face.
Il y a aujourd’hui plusieurs méthodes permettant de contourner ce problème et il n’y a pas une méthode qui fonctionne toujours mieux que l’autre. D’ailleurs, pour notre exemple, on constate que certaines techniques n’ont rien changé à la performance du modèle.
De manière générale, le plus important dans ce contexte est d’abord de bien choisir la métrique permettant d’évaluer le modèle et ensuite de tester de nombreuses techniques avant de retenir celle avec laquelle la performance de l’algorithme est la meilleure. On peut parfois aussi récupérer plus de données d'entraînement dans la mesure du possible.
Finalement, un problème de classification binaire avec un dataset extrêmement déséquilibré peut également être vu comme un problème de One-Class-Classification dont on pourra étayer les différentes techniques dans un prochain article.
Bibliographie
[1] https://www.kdnuggets.com/2017/06/7-techniques-handle-imbalanced-data.html
[2] https://blog.soat.fr/2019/12/techniques-augmentation-dataset-smote/
[3] https://towardsdatascience.com/fraud-detection-with-cost-sensitive-machine-learning-24b8760d35d9
[4] Imbalance-Aware Machine Learning for Predicting Rare and Common Disease-Associated Non-Coding Variants, Max Schubach, Matteo Re, Peter N Robinson and Giorgio Valentini
[5] https://pdfs.semanticscholar.org/5dd8/2357b16f9893ca95e29c65a8974fd94b55f4.pdf