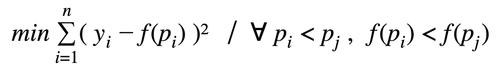Calibration de probabilité

Dans un article traitant des intervalles de prédiction, nous avions abordé une technique de mesure d’incertitude en régression. Qu’en est-il de cette mesure pour l’autre pan de l’apprentissage supervisé : la classification ?

En classification aussi, il convient de pouvoir maîtriser le niveau de confiance dans la sortie des modèles. Prenons l’exemple canonique de la classification binaire des tumeurs (maligne / bénigne) en fonction de leur taille. On aimerait pouvoir affirmer que si la probabilité en sortie est 0.3, on a effectivement un risque de 30% que la tumeur soit maligne. Cela est loin d’être le cas dans la pratique pour de nombreux algorithmes.

Citons deux exemples où avoir une probabilité calibrée est nécessaire :

• En marketing, on évalue ce que rapporte un client tout au long de la période durant laquelle il reste fidèle à l’entreprise : la CLV. Il est alors courant de multiplier le prix d’un produit par la probabilité qu’il a d’être acheté : CLV = 200€ x 0.1 = 20€.
• En médecine, certains résultats sont sensibles. L’ordre des probabilités d’avoir un cancer importe peu les patients. En revanche, une probabilité ayant un sens physique est vitale.

Les modèles non calibrés sont une plaie lorsqu’il s’agit de vouloir interpréter le résultat de predict_proba. L’abstraction de cette méthode - que l’on a tendance à utiliser sans comprendre ce qu’il y a derrière - est très dangereuse quand on voit les soucis de calibration que nous allons illustrer dans la première partie.

Néanmoins, des méthodes existent pour pallier les écueils de calibration comme la régression isotonique que nous détaillerons en seconde partie.

Le code utilisé est disponible ici et là.

Les courbes de calibration

Contrairement à la régression qui permet d’estimer une variable continue, la classification retourne une probabilité d’appartenir à une classe C. On dit de la variable cible Y qu’elle est discrète. En notant les variables explicatives X, on cherche la probabilité conditionnelle pour Y d’appartenir à la classe C sachant X : P(Y=C|X).

Comment interprète-t-on cette probabilité ? Sans s’attarder sur l'épistémologie de ce terme, notons qu’il peut signifier à la fois la chance qu’un événement a de se réaliser d’un point de vue fréquentiste, mais aussi le degré de croyance en la réalisation de l’événement en présence d’incertitude. Par souci de simplicité, nous confondrons ces deux notions dans la suite de cet article.

En suivant notre raisonnement, pour accéder au degré d’incertitude de notre modèle de classification, il est nécessaire que les probabilités en sortie soient bien calibrées. Cela signifie que la proportion d’individus ayant une même probabilité d’appartenir à une classe est égale à cette probabilité. Comme vu en introduction, si l’on prend tous les individus ayant une probabilité P=0.3 d’appartenir à la classe C = « tumeur maligne », environ 30% d’entre eux doivent effectivement avoir une tumeur maligne.

Néanmoins, les classifieurs ne sont que rarement calibrés. Il existe un moyen de mesurer la qualité d’un estimateur sur cet aspect : la courbe de calibration [1]. Elle est implémentée dans la bibliothèque scikit-learn. L’algorithme est le suivant :

• découper l’axe[0, 1]en plusieurs intervalles
• sélectionner les individus dont la probabilité appartient à chaque intervalle
• calculer la proportion d’individu appartenant à la classe C

Ce code permet de générer les figures 1 et 2.

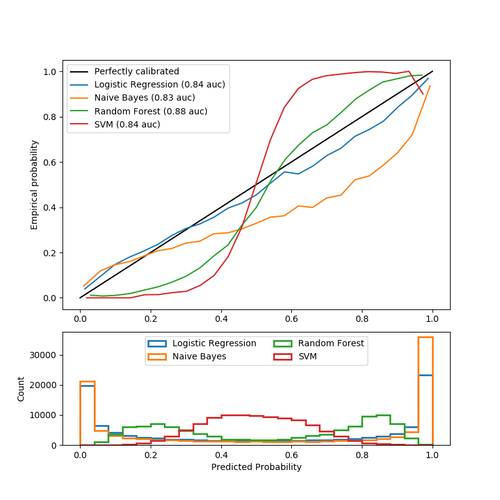
Figure 1 : Courbes de calibration pour 4 classifieurs

Cette figure illustre les écueils des résultats des méthodes appelées predict_proba dans les algorithmes de classification classiques. Les données sont simulées à l’aide de la méthode make_classification et les classifieurs ont été réglés pour avoir un score d’auc comparable.

• La droite noire représente la calibration parfaite : pour chaque groupe d’individu ayant une probabilité prédite similaire, la proportion (probabilité empirique) de ces individus étant vraiment dans la classe 1 est égale à la probabilité prédite.
• La régression logistique est le modèle le mieux calibré sur cette figure : il est proche de la droite noire. C’est en effet un cas particulier des modèles linéaires généralisés. Une loi de probabilité (Bernoulli) est associée à la réponse Y. Le modèle donne donc des probabilités au sens statistique par hypothèse de construction.
• La classification naïve bayésienne voit déjà ses probabilités moins bien calibrées, surtout celles proches de 1. En fait, ce modèle renvoie bien des probabilités mais l’hypothèse dite “naïve” d’indépendance des variables explicatives n’est en pratique jamais respectée (2 variables sont d’ailleurs redondantes dans les données simulées). Cette sigmoïde transposée traduit la sur-confiance de l’algorithme en ses prédictions. Pour les individus prédits à 0.8, seuls 50% appartiennent en fait à la classe 1.
• La forêt d’arbre aléatoire montre un histogramme ayant des pics de probabilité à 0.2 et 0.8, alors que les probabilités proches de 0 ou 1 sont très rares. En effet, le fait de moyenner des prédictions d’arbres de décision comprises entre 0 et 1 empêche de trouver des valeurs extrêmes (il faudrait que tous les classifieurs faibles soient d’accord sur les valeurs extrêmes, ce qui est très rare à cause du bagging qui crée du bruit). En conséquence, on observe une sigmoïde indiquant que le classificateur pourrait faire davantage confiance à son intuition et rapprocher les probabilités de 0 et 1.
• La machine à vecteurs de support n’a pas de méthode predict_proba mais une méthode decision_function qui renvoie comme indice de confiance la distance à l’hyperplan séparateur (i.e: frontière de décision). Cette distance (non comprise entre 0 et 1) n’est pas une probabilité et on s’en rend bien compte en observant à nouveau une sigmoïde encore plus éloignée de la droite noire.

Figure 2 : Courbes de calibration

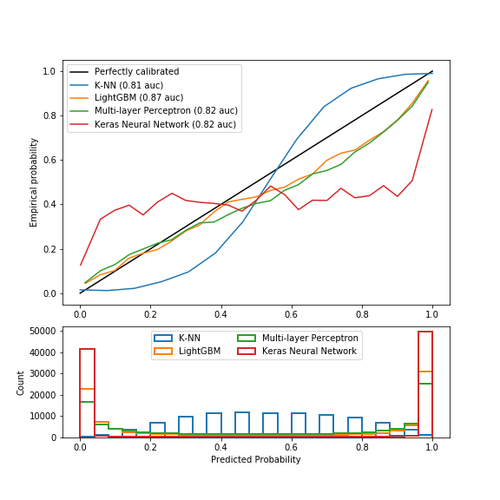
Cette seconde figure est similaire à la première avec d’autres algorithmes, la séparation ayant été effectuée par souci de clarté.

• La méthode des k plus proches voisins montre à nouveau une sigmoïde. En effet la méthode predict_proba représente à nouveau un concept particulier de probabilité. C’est la moyenne des classes les plus proches pondérée par l’inverse de la distance. Par exemple, si k=15, douze plus proches voisins sont des 1 et trois sont des 0, tous étant à égale distance, alors la probabilité d’appartenir à la classe 1 serait 12/15=0.8.
• L’algorithme LightGBM est une méthode ensembliste de boosting. Les probabilités ne sont pas mauvaises du fait de l’optimisation de la fonction de coût logloss.
• Le perceptron est assez bien calibré car il n’est composé que d’une seule couche de 100 neurones. Ainsi, la fonction apprise est linéaire. En outre, l’activation en sortie est une sigmoïde, qui approxime bien des probabilités.
• Le réseau de neurone Keras est composé de 2 couches, l’architecture est plus complexe, la fonction n’est plus linéaire. Depuis plusieurs années, les performances des réseaux ont explosé, la complexité de leurs architectures aussi. Les techniques utilisées pour éviter les problèmes de vanishing gradient et dying ReLu [2] ont dégradé la calibration des probabilités [3].

N.B: Les techniques de sous ou sur-échantillonnage, pour répondre aux problèmes de classes déséquilibrées, modifient la distribution de probabilité a priori et engendrent des probabilités très mal calibrées.

Comment faire pour éviter ce problème récurrent de calibration ?

La régression isotonique

Détaillons une des techniques existantes, proposées initialement dans [4] : la calibration par régression isotonique. Le principe est le suivant :

• Entraîner un modèle de classification
• Tracer la courbe de calibration
• Si les probabilités ne sont pas calibrées, entraîner une régression isotonique prenant en entrée X les probabilités prédites par le modèle et en cible y les cibles réelles associées
• Calculer les probabilités calibrées en composant la régression isotonique et le modèle :

p=isotonic regression ( model (X) )

Voici un exemple de code python qui permet de calibrer les probabilités d’un classifieur naïf bayésien :

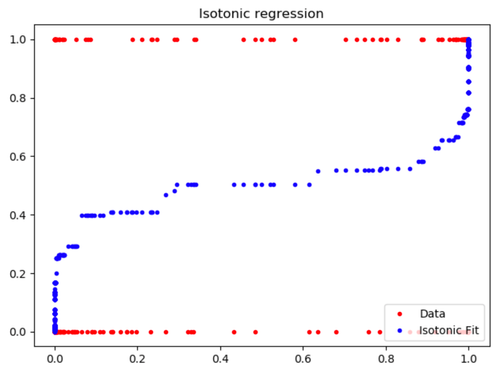
Figure 3 : Résultat de la régression isotonique

La régression isotonique entraînée épouse bien la forme de calibration du classifieur naïf bayésien. Ainsi, si le classifieur renvoie une probabilité de 0.2, notre modèle calibré retournera environ une probabilité de 0.4.

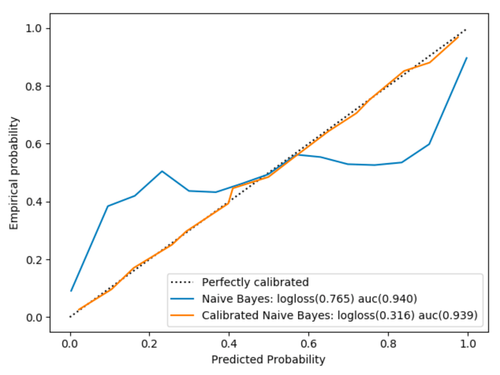
Figure 4 : Comparaison des probabilités avant et après calibration

La classe CalibratedClassifierCV permet de faire cela de façon concise, mais il semblait intéressant de le détailler dans le code par souci de compréhension. Sur la figure 3, outre la différence de calibration entre le modèle simple et celui calibré par régression isotonique, on voit que le score logloss est nettement meilleur lorsque les probabilités sont calibrées (cela est vrai seulement pour les modèles qui n’optimisent pas directement cette fonction de coût). En revanche, le score en auc n’est quasiment pas modifié car cette métrique ne dépend que de l’ordre des probabilités et la régression isotonique possède une contrainte de monotonie.

La régression isotonique est une fonction f, non paramétrique, croissante, qui, une fois entraînée, envoie un vecteur de probabilités vers un vecteur de probabilités calibrées tel que  .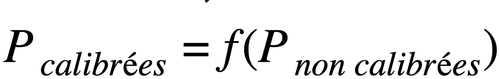

Trouver f revient à minimiser les moindres carrés tout en imposant une contrainte de monotonie, ou plus formellement, à résoudre le problème suivant :

L’algorithme utilisé - que nous nous contenterons d’illustrer [5] - s’appelle PAVA (Pool Adjacent Violators Algorithm) et a une complexité linéaire. Il prend en entrée le vecteur des cibles réelles yiordonné par probabilité croissante (sortie du classifieur).

Ce snippet de code permet de générer la figure suivante :

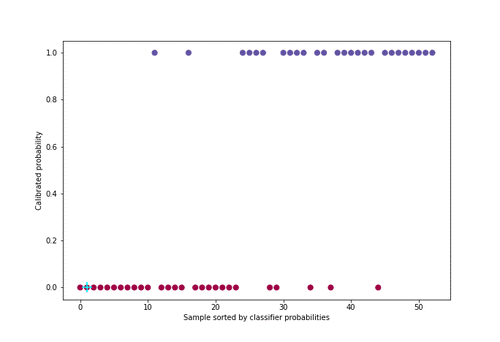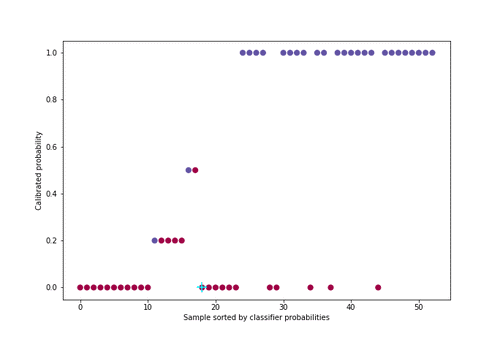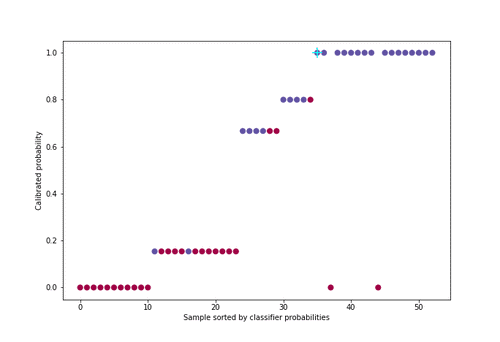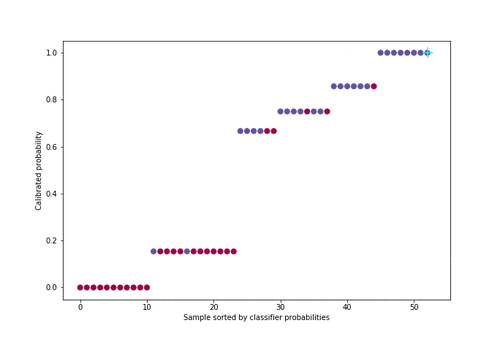
Figure 5 : Animation de la calibration avec l’algorithme PAVA

Pour une meilleure visualisation, environ 50 individus ont été sélectionnés uniformément dans la distribution de probabilité parmi les 21000 de l’ensemble de validation croisée.

Cette méthode a comme avantage par rapport à d’autres de bien calibrer les probabilités quel que soit le défaut de calibration du classifieur (sur ou sous-confiance en lui). En revanche, la condition pour bien fonctionner est que l’on doit disposer de suffisamment de données puisqu’il y a deux étapes d’apprentissage, une première pour le classifieur et une seconde pour la régression isotonique.

Conclusion

A retenir :

• Estimer l’incertitude est possible en classification : il convient de vérifier dans un premier temps la qualité des probabilités puis de les calibrer si nécessaire.
• La calibration fait correspondre la sortie des méthodes predict_proba à l’intuition physique qu’on a d’une probabilité, ce qui permet d’ajuster les actions à prendre.
• Les modèles qui n’optimisent pas la logloss ou les problèmes de données déséquilibrées donnent souvent des probabilités mal calibrées.
• A score équivalent, on préférera un modèle qui a confiance en lui lorsque les probabilités sont calibrées (i.e les probabilité sont proches de 0 et de 1).

Quelques pistes de réflexion pour le futur :

1. Il conviendrait de considérer le cas multiclasse. Une première approche possible est de considérer le problème comme autant de classifications binaires qu’il y a de classes.
2. D’autres méthodes existent :
   1. Deux algorithmes paramétriques (utiles lorsque trop peu de données sont disponibles pour les méthodes non-paramétriques)
      1. La sigmoïde si le classifieur n’a pas assez confiance dans ses prédictions (SVM par exemple).
      2. La beta calibration si à l’inverse le classifieur a trop confiance en lui.
   2. Deux algorithmes non-paramétriques
      1. Un algorithme basé sur les splines cubiques qui gère le cas multiclasse et peut être plus fin dans la calibration par rapport à la régression isotonique qui renvoie des morceaux de fonctions constantes [6].
      2. Le Bayesian Binning [7] qui essaie de résoudre le problème de la possible non-monotonie de la courbe de calibration.
3. Enfin, l’apprentissage bayésien, sujet très en vogue, s’attaque aux réseaux de neurones et offre une nouvelle approche basée sur la notion d’incertitudes. La librairie TensorFlow Probability offre la possibilité d’apprendre les paramètres des distributions pour prédire cette incertitude.

Références

[1] https://jmetzen.github.io/2015-04-14/calibration.html

[2] Dying ReLU and Initialization: Theory and Numerical Examples. Lu Lu, Yeonjong Shin, Yanhui Su, George Em Karniadakis. 2019

[3] On Calibration of Modern Neural Networks. Chuan Guo, Geoff Pleiss, Yu Sun, Kilian Q. Weinberger. 2018

[4] Transforming Classifier Scores into Accurate Multiclass Probability Estimates. Bianca Zadrozny and Charles Elkan. 2002

[5] http://fa.bianp.net/blog/2013/isotonic-regression/

[6] Spline-Based Probability Calibration. Brian Lucena. 2018

[7] Obtaining Well Calibrated Probabilities Using Bayesian Binning. Mahdi Pakdaman, Gregory F. Cooper, and Milos Hauskrecht. 2015