Lors d'un projet de datascience, il n'est pas rare de proposer un certain nombre de métriques pour évaluer des modèles de machine learning. Ces métriques sont censées quantifier le niveau de la prédiction et donner une idée plus ou moins précise de la qualité du pattern obtenu. Or ces métriques, issues du monde des statistiques, ne fournissent pas toujours d'interprétation métier immédiate et restent donc cantonnées au statut de nombre abstrait. Cet article a pour objectif d'expliquer ces métriques du point d'un point de vue métier, avec quelques exemples concrets et illustrés.

Contexte

Pour cet article, nous nous restreindrons aux modèles de classification binaire. Ce type de prédiction est effectivement assez fréquent lorsqu'il s'agit de prendre une décision marketing (le client va acheter), online advertising (le client va cliquer sur une publicité), industrie (le vol va être en retard) ou encore en text mining (ce mail est un spam, ce document est invalide).

Considérant que l'objet de l'étude est le client (d'une banque ou d'une assurance par exemple), un modèle de machine learning de classification binaire a besoin de deux inputs que sont :

• Les caractéristiques du client (identitaires, sociologiques, comportementales, etc...) dites données d'apprentissage
• Un fait bien précis en rapport avec le client dit cible d'apprentissage

Pour chaque client, les données utilisées ne doivent pas être postérieures au moment de sa décision. Le risque serait d'introduire des biais très subtils conduisant à un sur-apprentissage du modèle. La conséquence est que le modèle construit de cette manière sera moins performant lors du passage en production.

Le modèle de classification binaire ressortira un output lorsqu'il sera nourri de nouvelles données de test.

• Un score pour chaque client. Ce score peut aussi être considéré ou transformé si besoin en probabilité. Il correspond à la confiance accordée par le modèle au fait que le client soit classifié 1, c'est-à-dire par exemple le client va acheter.
• Chaque score peut être seuillé pour séparer les deux classes et obtenir des prédictions. La prédiction est souvent l'output final du modèle de datascience car elle permettra la prise de décision opérationnelles.

Métriques

Nous pouvons désormais confronter ces probabilités et prédictions à la réalité du terrain (le client a-t-il vraiment acheté ?) pour construire ces métriques qui constituent l'aboutissement d'une itération de datascience.

Il existe grosso modo deux manières d'exploiter ces probabilités. Prendre une métrique qui applique un seuil sur les probabilités pour obtenir des prédictions ou prendre une métrique qui se base directement sur les probabilités.

Matrice de confusion

L'objet de l'étude est à présent le vol. Supposons que vous avez demandé à l'équipe de datascientists de prédire quels vols internationaux du prochain mois seront en retard parmi 1000 vols. L'équipe a produit les probabilités pour chaque vol et vous remet cette liste pour action opérationnelle. Vous décidez de prendre un seuil arbitraire à 0.5 et de l'appliquer aux probabilités pour obtenir des prédictions sur les 1000 vols :

• 200 vols ont été prédits en retard (car leur probabilité était supérieure ou égale à 0.5)
• 800 vols ont été prédits à l'heure (car leur probabilité était inférieure à 0.5)

Un mois plus tard, vous décidez de confronter ces chiffres à la réalité du terrain et constatez que :

• Parmi les 200 vols prédits en retard, 50 ont effectivement été en retard
• Parmi les 800 vols prédits à l'heure, 700 ont été à l'heure

Vous venez de produire ce qu'on appelle une matrice de confusion. Celle-ci résume rapidement la qualité du classifieur en regardant les cases diagonales (bonnes prédictions) et les cases non diagonales (mauvaises prédictions) :

Attention, dans l'article Wikipédia français, les colonnes correspondent aux prédictions et les lignes à la réalité, alors que c'est l'inverse dans l'article Wikipédia anglais.

Insatisfait car trop de vols en retard ont été oubliés et prédits à l'heure, vous décidez de diminuer le seuil et obtenez cette nouvelle matrice de confusion :

Les vrais positifs (vols en retard et prédits en retard) sont passés de 50 à 90. Les faux négatifs (vols en retard et prédits à l'heure) ont diminué passant de 100 à 60.

Sans le savoir, vous avez cherché à augmenter le recall, mesure de la capacité de votre classifieur à ne pas oublier des vols en retard. La contrepartie est de perdre en précision. En effet, car pour récupérer plus de vols en retard dans la prédiction en retard, il a fallu prendre plus de risques et donc prédire en retard plus de vols qu'avant (90+200 contre 50+150 avant). Le seuil est plus lâche et la prédiction est moins précise : 200 faux positifs (vols à l'heure et prédits en retard) contre 150 avant.

Précision-recall

Le recall obtenu de cette deuxième matrice de confusion correspond à :

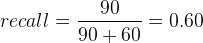
La précision sera elle de :

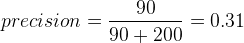
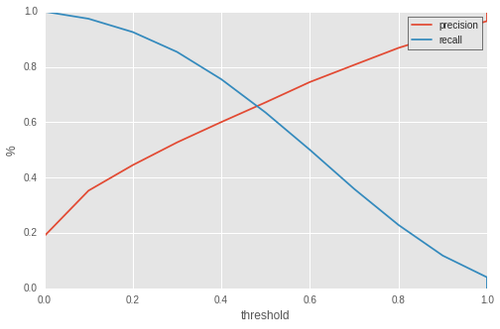
Il est ainsi possible de définir une précision et un recall pour chaque seuil. On obtient de cette manière une courbe dite precision-recall qui traduit le comportement global du classifieur. Voici un example de courbe precision-recall :

En abscisse se trouve le seuil. Un seuil de 0 signifie que tous les vols sont prédits en retard. Le recall est maximal donc égal à 1 et la précision minimale. A l'inverse, un seuil établi à 1 signifie que le classifieur prédira tous les vols à l'heure. Le recall est nul car aucun vol en retard n'a été prédit en retard et la précision tend vers 1 car n'ayant pris aucun risque, le classifieur ne s'est jamais trompé concernant les vols prédits en retard (car il n'y en a pas).

Il y a fondamentalement une bonne explication aux directions opposées que prennent ces deux courbes : Le biais exploration/exploitation. Pour un classifieur donné, vous pouvez choisir d'exploiter sans prendre de risques à savoir choisir un petit nombre de vols dont on sera sur qu'ils vont être en retard. La précision sera très bonne mais le recall faible. A l'inverse, vous pouvez décider de prendre plus de risques et d'explorer des zones où le classifieur n'est pas parfait. Diminuer le seuil revient à aller dans ce sens. Pour illustrer ce principe, voici la métaphore des flèchettes :

Considérons la tâche de lancer des fléchettes sur les zones noires ainsi qu'un cercle (en blanc) qui sera votre zone exclusive de visée. Plus le cercle est grand et plus il est possible de placer de nombreuses fléchettes dans les zones noires et donc de mettre des points. Mais le risque de se tromper est d'autant plus grand et un mauvais lanceur fera beaucoup d'erreurs. A l'inverse plus le cercle est petit et plus c'est simple de ne pas se tromper. La contrepartie est qu'il n'est possible de placer que quelques fléchettes.

Dans cet exemple, le seuil est représenté par le rayon du cercle blanc. Un seuil très élevé donc très strict correspond à un cercle tout petit.

Inversement un très bon classifieur/lanceur ne fera que peu d'erreurs même avec des cercles plus grands.

Ceci nous amène donc à des métriques qui sont indépendantes de tout seuil

AUC : Area Under Curve

Pour chaque seuil, nous avions des métriques qui résumaient la performance de notre classifieur. Nous allons désormais utiliser une métrique géométrique définie par l'aire sous la courbe. Mais quelle courbe ? Plusieurs possibilités s'offrent à nous :

Precision-Recall AUC (PR AUC)

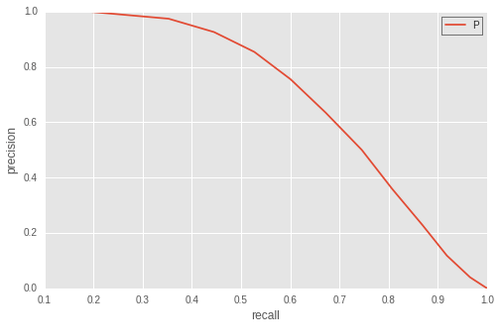
Pour chaque seuil, nous disposons d'une valeur de la précision et du recall. Nous pouvons donc tracer la courbe paramétrique de la precision en fonction du recall pour tous les seuils de 0 à 1. Cette courbe part du point (precision, recall) = (0,1) jusqu'au point (precision, recall) = (1,0). En voici un exemple concret pour une AUC d'environ 0.71 :

Plus une courbe a un profil qui se rapproche du point parfait (precision, recall) = (1,1) et meilleur sera le classifieur. L'aire en-dessous de cette courbe est alors une mesure naturelle de la performance globale du classifieur.

Une interprétation de cette PR AUC serait la suivante

Supposons que vous choisissiez au hasard un vol prédit en retard ainsi que, toujours au hasard, un vol en retard. L'AUC est alors la probabilité que le vol prédit en retard soit mieux classé en terme de probabilités que le vol en retard.

D'une certaine façon, c'est une mesure de la confiance qu'a le classifieur dans ses propres prédictions du retard par rapport à la réalité.

Receiver Operating Characteristic AUC (ROC AUC)

Nous pouvons également remplacer la précision par une autre mesure pour obtenir la courbe ROC : le fall-out ou taux de faux positifs. Si nous reprenons notre première matrice de confusion :

Nous pouvons recalculer le recall :

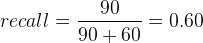
et le taux de faux positifs cette fois-ci :

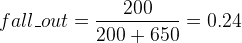
à mettre en opposition avec la précision qui n'est plus la métrique qui nous interesse :

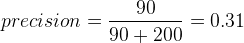
L'apparition du terme 650 montre que cette nouvelle mesure tient compte des vrais négatifs, ie des vols à l'heure et prédits à l'heure. Elle est donc sensible à notre capacité à prédire à l'heure tandis que le recall mesurera notre capacité à prédire le retard.

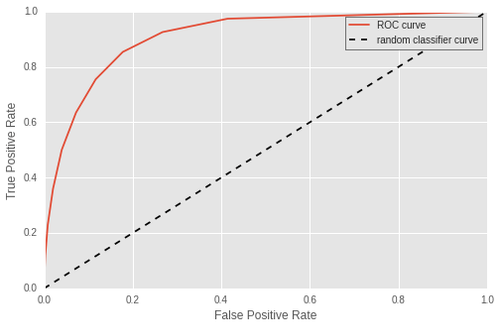
Voici la courbe ROC (recall en fonction du fall_out) correspondante :

En légende, le True Positive Rate est le recall et le False Positive Rate est le fall_out. Cette fois-ci, la courbe va du point (recall, fall_out) = (1,1) correspondant à un seuil de 0 jusqu'au point (recall, fall_out) = (0,0) pour un seuil de 1 . En effet car pour un seuil de 0, le recall est toujours maximal comme énoncé précédemment, et le fall_out maximal puisque tous les vols à l'heure ont été mal prédits. A l'inverse, le seuil de 1 correspond à un classifieur très strict, le recall est nul puisque tous les vols sont déclarés à l'heure mais le fall_out est parfait car nul également.

De la même façon, plus la courbe s'approche du point (1,0) ie recall égal à 1 et fall_out nul et meilleur est le classifieur. L'AUC est une métrique tout aussi naturel pour cette courbe. Ici, l'AUC de cette courbe ROC est de 0.91.

Intuitivement, elle correspond ici à :

Si vous prenez au hasard un vol en retard et un vol à l'heure, l'AUC correspond à la probabilité que votre classifieur donne un meilleur rang au vol en retard qu'au vol à l'heure. Une AUC égale à 1 signifie que les vols en retards auront toujours une meilleure probabilité individuelle (ou score) que les vols à l'heure. Il existera donc un seuil pour lequel les prédictions binaires du classifieur sont parfaites.

La ROC AUC est donc la capacité du classifieur à distinguer entre les deux cibles retard et à l'heure.

Quelques considérations sur les datasets fortement déséquilibrés

Il est très courant de choisir la ROC AUC comme métrique dès lors qu'on veut étudier la performance d'un classifieur binaire. Mais lorsque la classe positive vols en retard est moins fréquente que la classe négative vols à l'heure, il est plus intéressant de prendre la PR AUC comme métrique [1]. Les métriques de précision-recall ne s'occupent pas des vrais négatifs, ie ici des vols à l'heure et prédits à l'heure. Lorsque ceux-ci sont très nombreux, ils ne viennent pas perturber les graphe et changer l'AUC. A l'inverse, la ROC AUC a comme composante le fall_out qui prend en compte les vrais négatifs. Ceux-ci ont un effet non négligeable sur la tenue de la métrique en fonction du niveau de déséquilibre du dataset.

Conclusion

Mesurer la performance d'un classifieur et de ce fait la production d'une équipe de datascience n'est pas chose aisée. Un même classifieur peut être bon pour une métrique et mauvais pour une autre. Choisir en avance de phase une métrique qui correspond le mieux à une éventuelle action métier sur les prédictions ou à un gain financer potentiel est essentiel. Cela peut être par exemple une AUC ou un recall à précision fixée. Il est donc fondamental de s'approprier la métrique utilisée car elle est d'une certain manière la passerelle entre la modélisation théorique et la réalité.

Bibliographie

[1] http://dl.acm.org/citation.cfm?id=1143874